Question

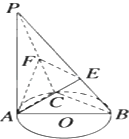
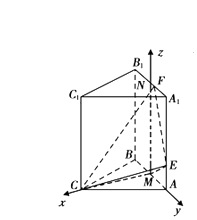
【题目】在三棱柱ABC﹣A1B1C1中，CA=CB，侧面ABB1A1是边长为2的正方形，点E，F分别在线段AAl ， A1B1上，且AE= ，A1F= ，CE⊥EF，M为AB中点 （Ⅰ）证明：EF⊥平面CME；
（Ⅱ）若CA⊥CB，求直线AC1与平面CEF所成角的正弦值．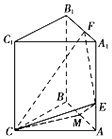

Answer 1

【答案】证明：（Ⅰ）在正方形ABB1A1中，A1E= ，AM=1， 在Rt△EAM和Rt△FA1E中， ，
又∠EAM=∠FA1E= ，∴Rt△EAM∽Rt△FA1E，
∴∠AEM=∠A1FE，∴EF⊥EM，
又EF⊥CE，ME∩CE=E，∴EF⊥平面CEM．
解：（Ⅱ）在等腰三角形△CAB中，
∵CA⊥CB，AB=2，∴CA=CB= ，且CM=1，
设线段A1B1中点为N，连结MN，由（Ⅰ）可证CM⊥平面ABB1A1 ，
∴MC，MA，MN两两垂直，
建立如图所示的空间直角坐标系，
则C（1，0，0），E（0，1， ），F（0， ，2），A（0，1，0），C1（1，0，2），
=（﹣1，1， ）， =（0，﹣ ， ）， =（1，﹣1，2），
设平面CEF的法向量为 =（x，y，z），
则 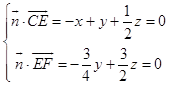，取z=2，得 =（5，4，2），
设直线AC1与平面CEF所成角为θ，
则sinθ= = ，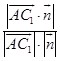
∴直线AC1与平面CEF所成角的正弦值为 ．

【解析】（Ⅰ）推导出Rt△EAM∽Rt△FA1E，从而EF⊥ME，又EF⊥CE，由此能证明EF⊥平面CEM．（Ⅱ）设线段A1B1中点为N，连结MN，推导出MC，MA，MN两两垂直，建空间直角坐标系，利用向量法能求出直线AC1与平面CEF所成角的正弦值．