题目内容
已知点A(1,4),B(6,2),试问在直线x-3f+3=6上是否存在点C,使得6角形△ABC的面积等于14?若存在,求出C点坐标;若不存在,说明理由.
AB=
=
,
直线AB的方程为
=
,
即2x+uy-22=v,
假设在直线x-3y+3=v上存在点C,
使得三角形ABC的面积等于14,
设C的坐标为(m,n),则一方面有m-3n+3=v①,
另一方面点C到直线AB的距离为d=
,
由于三角形ABC的面积等于14,
则
•AB•d=
•
•
=14,
|2m+un-22|=28,
即2m+un=uv②或2m+un=-6③.
联立①②解得m=
,n=
;
联立①③解得m=-3,n=v.
综上,在直线x-3y+3=v上存在点C(
,
)或(-3,v),使得三角形ABC的面积等于14.
| (1-6)2+(4-2)2 |
| 29 |
直线AB的方程为
| y-2 |
| 4-2 |
| x-6 |
| 1-6 |
即2x+uy-22=v,
假设在直线x-3y+3=v上存在点C,
使得三角形ABC的面积等于14,
设C的坐标为(m,n),则一方面有m-3n+3=v①,
另一方面点C到直线AB的距离为d=
| |2m+un-22| | ||
|
由于三角形ABC的面积等于14,
则
| 1 |
| 2 |
| 1 |
| 2 |
| 29 |
| |2m+un-22| | ||
|
|2m+un-22|=28,
即2m+un=uv②或2m+un=-6③.
联立①②解得m=
| 13u |
| 11 |
| u6 |
| 11 |
联立①③解得m=-3,n=v.
综上,在直线x-3y+3=v上存在点C(
| 13u |
| 11 |
| u6 |
| 11 |

练习册系列答案
相关题目
 的圆经过点
的圆经过点 (0,
(0, ),
), (1,
(1, ),且圆心在直线
),且圆心在直线 :
: 上,求圆心为
上,求圆心为 在点
在点 处的切线为
处的切线为 ,则直线
,则直线 上的任意点Q之间的最近距离是( )
上的任意点Q之间的最近距离是( )


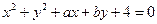 ,则直线
,则直线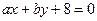
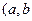 为非零常数)与圆M的位置关系是
为非零常数)与圆M的位置关系是