题目内容
已知函数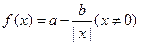 。
。
(1)若函数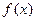 是
是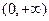 上的增函数,求实数
上的增函数,求实数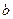 的取值范围;
的取值范围;
(2)当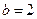 时,若不等式
时,若不等式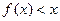 在区间
在区间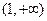 上恒成立,求实数
上恒成立,求实数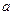 的取值范围;
的取值范围;
(3)对于函数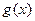 若存在区间
若存在区间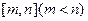 ,使
,使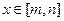 时,函数
时,函数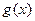 的值域也是
的值域也是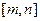 ,则称
,则称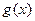 是
是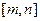 上的闭函数。若函数
上的闭函数。若函数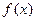 是某区间上的闭函数,试探求
是某区间上的闭函数,试探求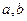 应满足的条件。
应满足的条件。
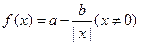 。
。(1)若函数
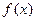 是
是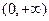 上的增函数,求实数
上的增函数,求实数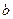 的取值范围;
的取值范围;(2)当
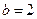 时,若不等式
时,若不等式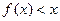 在区间
在区间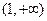 上恒成立,求实数
上恒成立,求实数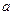 的取值范围;
的取值范围;(3)对于函数
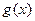 若存在区间
若存在区间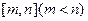 ,使
,使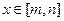 时,函数
时,函数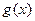 的值域也是
的值域也是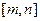 ,则称
,则称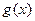 是
是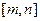 上的闭函数。若函数
上的闭函数。若函数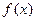 是某区间上的闭函数,试探求
是某区间上的闭函数,试探求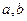 应满足的条件。
应满足的条件。(1)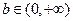 (2)
(2)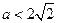 (3)
(3)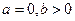
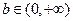 (2)
(2)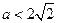 (3)
(3)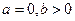
(1)当 时,
时,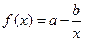
设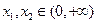 且
且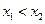 ,由
,由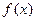 是
是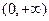 上的增函数,则
上的增函数,则 2分
2分
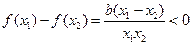 3分
3分
由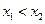 ,
,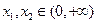 知
知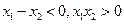 ,所以
,所以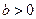 ,即
,即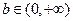 5分
5分
(2)当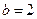 时,
时,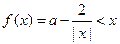 在
在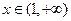 上恒成立,即
上恒成立,即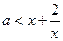 6分
6分
因为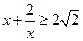 ,当
,当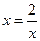 即
即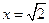 时取等号, 8分
时取等号, 8分
 ,所以
,所以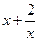 在
在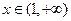 上的最小值为
上的最小值为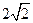 。则
。则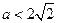 10分
10分
(3)因为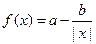 的定义域是
的定义域是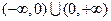 ,设
,设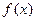 是区间
是区间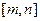 上的闭函数,则
上的闭函数,则 且
且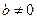 11分
11分
①若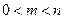
当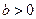 时,
时,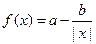 是
是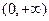 上的增函数,则
上的增函数,则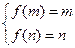 ,
,
所以方程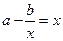 在
在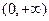 上有两不等实根,
上有两不等实根,
即 在
在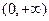 上有两不等实根,所以
上有两不等实根,所以
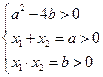 ,即
,即 且
且 13分
13分
当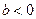 时,
时,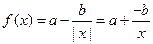 在
在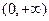 上递减,则
上递减,则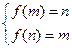 ,即
,即
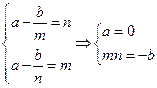 ,所以
,所以 14分
14分
②若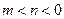
当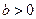 时,
时,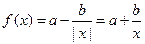 是
是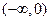 上的减函数,所以
上的减函数,所以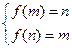 ,即
,即
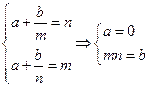 ,所以
,所以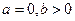 15分
15分
 时,
时,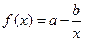
设
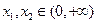 且
且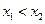 ,由
,由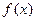 是
是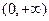 上的增函数,则
上的增函数,则 2分
2分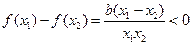 3分
3分由
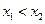 ,
,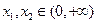 知
知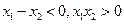 ,所以
,所以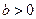 ,即
,即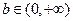 5分
5分(2)当
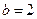 时,
时,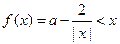 在
在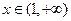 上恒成立,即
上恒成立,即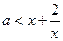 6分
6分因为
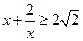 ,当
,当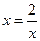 即
即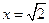 时取等号, 8分
时取等号, 8分 ,所以
,所以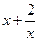 在
在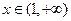 上的最小值为
上的最小值为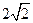 。则
。则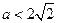 10分
10分(3)因为
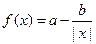 的定义域是
的定义域是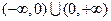 ,设
,设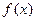 是区间
是区间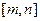 上的闭函数,则
上的闭函数,则 且
且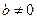 11分
11分①若
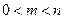
当
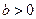 时,
时,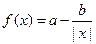 是
是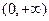 上的增函数,则
上的增函数,则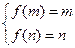 ,
,所以方程
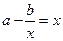 在
在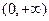 上有两不等实根,
上有两不等实根,即
 在
在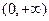 上有两不等实根,所以
上有两不等实根,所以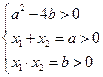 ,即
,即 且
且 13分
13分当
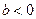 时,
时,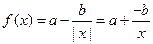 在
在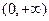 上递减,则
上递减,则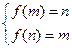 ,即
,即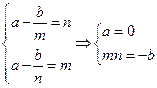 ,所以
,所以 14分
14分②若
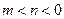
当
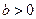 时,
时,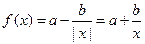 是
是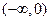 上的减函数,所以
上的减函数,所以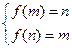 ,即
,即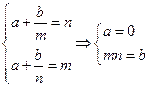 ,所以
,所以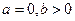 15分
15分
练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
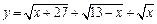 的最大和最小值.
的最大和最小值.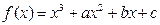 的一个零点为
的一个零点为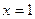 ,另外两个零点可分别作为一个椭圆、一个双曲线的离心率,求
,另外两个零点可分别作为一个椭圆、一个双曲线的离心率,求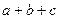 的值,及
的值,及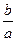 的取值范围
的取值范围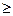 g(x)恒成立,求实数c的取值范围;
g(x)恒成立,求实数c的取值范围;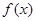 满足
满足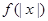 =|
=| ,且
,且 ,又知
,又知 恒成立,求
恒成立,求 的值.
的值.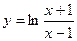 ,
,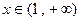 的反函数是【 】.
的反函数是【 】.
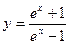
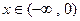
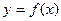 是偶函数,而
是偶函数,而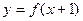 是奇函数,且对任意
是奇函数,且对任意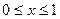 ,
,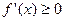 ,则
,则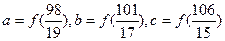 的大小关系是
的大小关系是



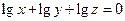 ,则
,则 .
.