题目内容
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)求函数![]() 的单调区间;
的单调区间;
(Ⅲ)若对任意的![]() ,都有
,都有![]() 成立,求a的取值范围.
成立,求a的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)当
(Ⅱ)当![]() 时增区间为
时增区间为![]() 当
当![]() 时增区间为
时增区间为![]() ,减区间为
,减区间为![]() (Ⅲ)
(Ⅲ)![]()
【解析】
试题(Ⅰ)利用导数的几何意义得到切线的斜率,进而得到切线方程(Ⅱ)首先计算函数的导数,令导数大于零可得增区间,进而得到减区间,求解时注意对参数的取值范围分情况讨论(Ⅲ)不等式恒成立问题中求参数范围的一般采用分离参数的方法,转化为求函数的最值问题
试题解析:(Ⅰ)![]() 时,
时,![]()
![]()
曲线![]() 在点
在点![]() 处的切线方程
处的切线方程![]()
(Ⅱ)![]()
①当![]() 时,
时,![]() 恒成立,函数
恒成立,函数![]() 的递增区间为
的递增区间为![]()
②当![]() 时,令
时,令![]() ,解得
,解得![]() 或
或![]()
x | ( 0, |
| ( |
f’(x) | - | + | |
f(x) | 减 | 增 |
所以函数![]() 的递增区间为
的递增区间为![]() ,递减区间为
,递减区间为![]()
(Ⅲ)对任意的![]() ,使
,使![]() 成立,只需任意的
成立,只需任意的![]() ,
,![]()
①当![]() 时,
时,![]() 在
在![]() 上是增函数,
上是增函数,
所以只需![]()
而![]()
所以![]() 满足题意;
满足题意;
②当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是增函数,
上是增函数,
所以只需![]()
而![]()
所以![]() 满足题意;
满足题意;
③当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是减函数,
上是减函数,![]() 上是增函数,
上是增函数,
所以只需![]() 即可
即可
而![]()
从而![]() 不满足题意;
不满足题意;
综合①②③实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】某医院用光电比色计检查尿汞时,得尿汞含量(毫克/升)与消光系数如下表:
尿汞含量 | 2 | 4 | 6 | 8 | 10 |
消光系数 | 64 | 138 | 205 | 285 | 360 |
(1)作散点图;
(2)如果![]() 与
与![]() 之间具有线性相关关系,求回归线直线方程;
之间具有线性相关关系,求回归线直线方程;
(3)估计尿汞含量为9毫克/升时消光系数.
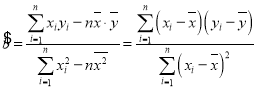 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.