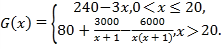题目内容
【题目】已知等差数列![]() 的首项为
的首项为![]() ,公差为
,公差为![]() ,前n项和为
,前n项和为![]() ,且满足
,且满足![]() ,
,![]() .
.
(1)证明![]() ;
;
(2)若![]() ,
,![]() ,当且仅当
,当且仅当![]() 时,
时,![]() 取得最小值,求首项
取得最小值,求首项![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据等差数列的前n项和公式,变形可证明![]() 为等差数列.结合条件
为等差数列.结合条件![]() ,
,![]() ,可得
,可得![]() ,进而表示出
,进而表示出![]() .由
.由![]() 为等差数列,表示出
为等差数列,表示出![]() ,化简变形后结合不等式性质即可证明
,化简变形后结合不等式性质即可证明![]() .
.
(2)将三角函数式分组,提公因式后结合同角三角函数关系式化简.再由平方差公式及正弦的和角与差角公式合并.根据条件等式,结合等差数列性质,即可求得![]() .由
.由![]() ,即可确定
,即可确定![]() .当且仅当
.当且仅当![]() 时,
时,![]() 取得最小值,可得不等式组,即可得首项
取得最小值,可得不等式组,即可得首项![]() 的取值范围.
的取值范围.
(1)证明:等差数列![]() 的前n项和为
的前n项和为![]() ,
,
则![]()
所以![]() ,
,![]() ,
,
故![]() 为等差数列,
为等差数列,
因为![]() ,
,![]() ,所以
,所以![]()
![]() ,解得
,解得![]() ,
,
因为![]() ,
,
得![]()
故![]() ,从而
,从而![]() .
.
(2)而![]()
![]()
![]()
![]()
![]() .
.
由条件![]()
又由等差数列性质知:![]()
所以![]() ,
,
因为![]() ,所以
,所以![]() ,那么
,那么![]() .
.
等差数列![]() ,当且仅当
,当且仅当![]() 时,
时,![]() 取得最小值.
取得最小值.
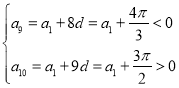 ,
,
所以![]() .
.

练习册系列答案
相关题目
【题目】某专卖店为了对新产品进行合理定价,将该产品按不同的单价试销,调查统计如下表:
售价 | 4 | 5 | 6 | 7 | 8 |
周销量 | 90 | 85 | 83 | 79 | 73 |
(1)求周销量y(件)关于售价x(元)的线性回归方程![]() ;
;
(2)按(1)中的线性关系,已知该产品的成本为2元/件,为了确保周利润大于598元,则该店应该将产品的售价![]() 定为多少?
定为多少?
参考公式: ,
,![]() .
.
参考数据:![]() ,
,![]()