题目内容
(本小题满分12分)
在如图所示的空间几何体中,△ABC,△ACD都是等边三角形,AE=CE,DE//平面ABC,平面ACD⊥平面ABC。
(1)求证:DE⊥平面ACD;
(2)若AB=BE=2,求多面体ABCDE的体积。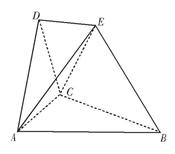
在如图所示的空间几何体中,△ABC,△ACD都是等边三角形,AE=CE,DE//平面ABC,平面ACD⊥平面ABC。
(1)求证:DE⊥平面ACD;
(2)若AB=BE=2,求多面体ABCDE的体积。

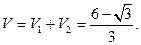
解:(1)法一:△ABC,△ACD都是等边三角形,
AE=CE,取AC中点O,连接BO,DO,EO,则
BO⊥AC,DO⊥AC,EO⊥AC ……………2分
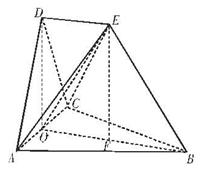
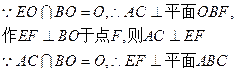
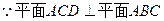 ,
,
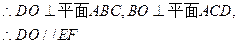
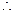 ODEF是平面四边形 ………………4分
ODEF是平面四边形 ………………4分
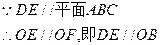
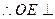 平面ACD ………………6分
平面ACD ………………6分
法二:△ABC,△ACD都是等边三角形,
AE=CE,取AC中点O,连接BO,DO,EO,则
BO⊥AC,DO⊥AC,EO⊥AC ……………2分
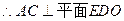 ,
, 平面OBE
平面OBE
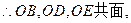 即OB,OD,OE
即OB,OD,OE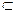 平面OBED
平面OBED
又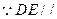 平面ABC,
平面ABC,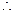 DE//BO ………………4分
DE//BO ………………4分
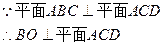
∴DE⊥平面ACD ………………6分
(2)由EF//DO,DE//OF,知DE=OF,EF=DO,
又AB=BE=2,△ABC,△ACD都是等边三角形,EF⊥BO
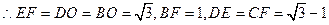 ………………8分
………………8分
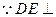 平面ACD,
平面ACD,
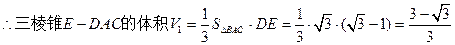 ;
;
又三棱锥E—ABC的体积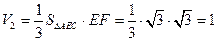 ………………11分
………………11分
∴多面体ABCDE的体积为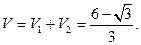 ………………12分
………………12分
AE=CE,取AC中点O,连接BO,DO,EO,则
BO⊥AC,DO⊥AC,EO⊥AC ……………2分

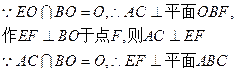
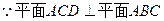 ,
,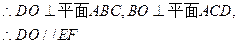
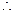 ODEF是平面四边形 ………………4分
ODEF是平面四边形 ………………4分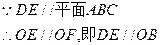
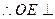 平面ACD ………………6分
平面ACD ………………6分法二:△ABC,△ACD都是等边三角形,
AE=CE,取AC中点O,连接BO,DO,EO,则
BO⊥AC,DO⊥AC,EO⊥AC ……………2分
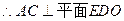 ,
, 平面OBE
平面OBE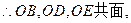 即OB,OD,OE
即OB,OD,OE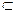 平面OBED
平面OBED又
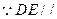 平面ABC,
平面ABC,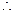 DE//BO ………………4分
DE//BO ………………4分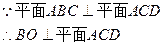
∴DE⊥平面ACD ………………6分
(2)由EF//DO,DE//OF,知DE=OF,EF=DO,
又AB=BE=2,△ABC,△ACD都是等边三角形,EF⊥BO
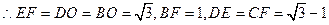 ………………8分
………………8分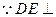 平面ACD,
平面ACD,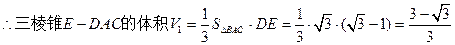 ;
;又三棱锥E—ABC的体积
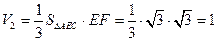 ………………11分
………………11分∴多面体ABCDE的体积为
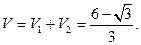 ………………12分
………………12分
练习册系列答案
相关题目
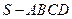 的底面是正方形,每条侧棱长都是底面边长的
的底面是正方形,每条侧棱长都是底面边长的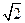 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。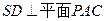 ,求二面角
,求二面角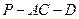 的大小;
的大小;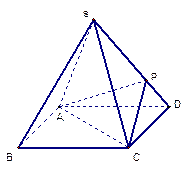
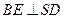 ,若存在,求
,若存在,求 的值;若不存在,试说明理由。
的值;若不存在,试说明理由。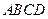 为矩形,
为矩形,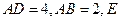 、
、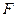 分别是线段
分别是线段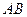 、
、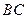 的中点,
的中点,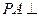 平面
平面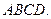 (1)求证:
(1)求证: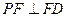 ;
;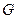 在
在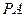 上,且
上,且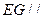 平面
平面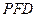 ,试确定点
,试确定点 ,
, 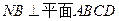 ,且MD=NB=1,E为BC 的中点 (1)求异面直线NE与AM所成角的余弦值
,且MD=NB=1,E为BC 的中点 (1)求异面直线NE与AM所成角的余弦值 平面AMN,并求线段AS的长;
平面AMN,并求线段AS的长;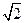 .
.
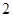 ,下底为
,下底为 ,高为
,高为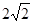 的等腰梯形,俯视图是两个半径分别为
的等腰梯形,俯视图是两个半径分别为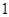 和
和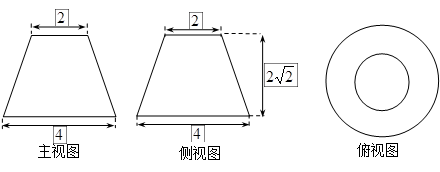
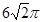
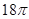
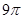
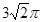
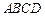 中,
中,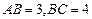 ,沿对角线
,沿对角线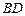 将
将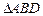 折起到
折起到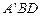 的位置,且
的位置,且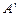 在平面
在平面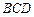 内的射影
内的射影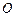 落在
落在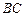 边上,则二面角
边上,则二面角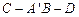 的平面角的正弦值为( )
的平面角的正弦值为( )

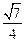
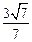
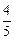
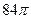 ,则圆台较小底面的半径为( )
,则圆台较小底面的半径为( )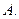 7
7  . 6
. 6 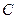 . 5
. 5 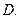 3
3