题目内容
若实数a、b满足a+b=2,是 的最小值是( )
的最小值是( )
| A.18 | B.6 | C.2 | D.2 |
B
解析试题分析:根据基本不等式可得 ,所以
,所以 的最小值是6.
的最小值是6.
考点:本小题主要考查基本不等式的应用.
点评:应用基本不等式时,要注意“一正二定三相等”三个条件缺一不可.

练习册系列答案
相关题目
半径为2的球面上有A,B,C,D四点,且AB,AC,AD两两垂直,则三个三角形面积之和 的最大值为( )
的最大值为( )
| A.4 | B.8 | C.16 | D.32 |
若 ,则下列不等式恒成立的是( )
,则下列不等式恒成立的是( )
A.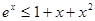 | B. |
C. | D. |
下列各式中,最小值等于 的是( )
的是( )
A. | B. | C. | D. |
函数 取得最小值时,
取得最小值时, 的值是( )
的值是( )
| A.1 | B.2 | C.3 | D.4 |
已知a+4b="ab," a、b均为正数,则使a+b>m恒成立的m的取值范围是
| A.m<9 | B.m≤9 | C.m<8 | D.m≤8 |
设 ,
, ,则
,则 三数 ( )
三数 ( )
| A.至少有一个不小于2 | B.都大于2 |
| C.至少有一个不大于2 | D.都小于2 |
 ,则方程
,则方程 (
( )的根的个数不可能为( )
)的根的个数不可能为( )  6
6  5
5  4
4  3
3 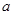 ,第三年增长率为
,第三年增长率为 ,则这两年平均增长率
,则这两年平均增长率 满足
满足


