题目内容
已知函数 ,则方程
,则方程 (
( )的根的个数不可能为( )
)的根的个数不可能为( )  6
6  5
5  4
4  3
3
A
解析试题分析:先画出函数f(t)的图象,得出f(t)=a的实数根的情况;再利用换元法,令t=2x2+x,进一步考查f(2x2+x)=a根的情况即可解:(1)画出f(x)图象,
当x>0时,f(x)=x+ ≥2,当x≤0时,f(x)=x3+3≤3.于是可得:①当2<a<3时,f(x)=a有3个根,一负二正;②当a=3时,f(x)=a有3个根,一零二正;③当3<a时,f(x)=a有2个正根;④当a=2时,f(x)=a有一正一负根;⑤当a<2时,f(x)=a只有一负根.(2)令t=2x2+x=2(x+
≥2,当x≤0时,f(x)=x3+3≤3.于是可得:①当2<a<3时,f(x)=a有3个根,一负二正;②当a=3时,f(x)=a有3个根,一零二正;③当3<a时,f(x)=a有2个正根;④当a=2时,f(x)=a有一正一负根;⑤当a<2时,f(x)=a只有一负根.(2)令t=2x2+x=2(x+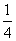 )2-
)2-
,则t≥- ,①当2<a<3时,f(t)=a有3个t使之成立,一负二正,两个正t分别对应2个x,当t<-
,①当2<a<3时,f(t)=a有3个t使之成立,一负二正,两个正t分别对应2个x,当t<- 时,没有x与之对应,当t=-
时,没有x与之对应,当t=- 时,有1个x与之对应,当t>-
时,有1个x与之对应,当t>- 时,有2个x与之对应,∴根的个数分别为4、5、6个;②当3<a时,f(t)=a有2个正根,两个正t分别对应2个x,此时根的个数为4个.③由题目不必考虑a≤2的情形.所以根的个数只可能为4、5、6个.即方程f(2x2+x)=a的根的个数只可能为4、5、6个,不可能为3个.故选A.
时,有2个x与之对应,∴根的个数分别为4、5、6个;②当3<a时,f(t)=a有2个正根,两个正t分别对应2个x,此时根的个数为4个.③由题目不必考虑a≤2的情形.所以根的个数只可能为4、5、6个.即方程f(2x2+x)=a的根的个数只可能为4、5、6个,不可能为3个.故选A.
考点:函数图象
点评:正确得出函数的单调性并画出函数图象、利用换元法及分类讨论的方法是解题的关键.

练习册系列答案
相关题目
已知正数 满足
满足 ,则
,则 的最小值为( )
的最小值为( )
A. | B.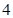 | C. | D. |
若 ,则对
,则对 说法正确的是
说法正确的是
A.有最大值 | B.有最小值 |
| C.无最大值和最小值 | D.无法确定 |
若 且
且 ,则下列不等式恒成立的是
,则下列不等式恒成立的是
A. | B. | C. | D. |
设 ,则有( )
,则有( )
A. | B. | C. | D. |
若a>1, 则  的最小值是 ( )
的最小值是 ( )
| A.2 | B.4 | C.1 | D.3 |
若实数a、b满足a+b=2,是 的最小值是( )
的最小值是( )
| A.18 | B.6 | C.2 | D.2 |
已知 则
则 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
若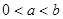 ,且
,且 ,则在下列四个选项中,最大的是( )
,则在下列四个选项中,最大的是( )
A. | B. | C. | D. |