题目内容
半径为2的球面上有A,B,C,D四点,且AB,AC,AD两两垂直,则三个三角形面积之和 的最大值为( )
的最大值为( )
| A.4 | B.8 | C.16 | D.32 |
B
解析试题分析:设AB=a,AC=b,AD=c,因为,半径为2的球面上有A,B,C,D四点,且AB,AC,AD两两垂直,所以,AB,AC,AD为球的内接长方体的一个角的三条棱.
故a2+b2+c2=16,
而 S△ABC+S△ACD+S△ADB= (ab+ac+bc)
(ab+ac+bc)
≤ 8.
8.
故选B.
考点:球及其内接几何体的特征,基本不等式的应用。
点评:小综合题,关键是发现AB,AC,AD为球的内接长方体的一个角的三条棱,得到a2+b2+c2=16,计算三个三角形的面积之和,利用基本不等式求最大值。

练习册系列答案
相关题目
若实数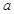 ,
, 满足
满足 ,则
,则 的最小值是
的最小值是
| A.18 | B.6 | C.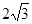 | D. |
已知实数 ,
, ,则
,则 的最小值是( )
的最小值是( )
A. | B. | C. | D. |
已知正数 满足
满足 ,则
,则 的最小值为( )
的最小值为( )
A. | B.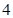 | C. | D. |
已知 与
与 互为反函数,若
互为反函数,若 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
若 ,则对
,则对 说法正确的是
说法正确的是
A.有最大值 | B.有最小值 |
| C.无最大值和最小值 | D.无法确定 |
若实数a、b满足a+b=2,是 的最小值是( )
的最小值是( )
| A.18 | B.6 | C.2 | D.2 |
若 ( )
( )
A. | B. | C. | D. |
 ,若直线
,若直线 与
与 轴相交于点
轴相交于点 ,与
,与 轴相交于点
轴相交于点 ,且坐标原点
,且坐标原点 到
到 的距离为
的距离为 ,则
,则 面积的最小值为( )
面积的最小值为( )


