题目内容
已知a+4b="ab," a、b均为正数,则使a+b>m恒成立的m的取值范围是
| A.m<9 | B.m≤9 | C.m<8 | D.m≤8 |
A
解析试题分析:由于已知中,a+4b="ab," a、b均为正数,则可知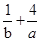 =1,使
=1,使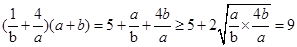 当且仅当
当且仅当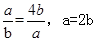 时取得等号,可知m<9,故选A.
时取得等号,可知m<9,故选A.
考点:均值不等式的运用
点评:解决该试题的关键是能利用和为定值来得到参数m的取值范围,属于基础题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若 ,则对
,则对 说法正确的是
说法正确的是
A.有最大值 | B.有最小值 |
| C.无最大值和最小值 | D.无法确定 |
若实数a、b满足a+b=2,是 的最小值是( )
的最小值是( )
| A.18 | B.6 | C.2 | D.2 |
已知 则
则 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
若 且2
且2 =2,则
=2,则 的最小值是( )
的最小值是( )
| A.2 | B.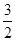 | C. | D. |
已知 ,则
,则 的最小值是( )
的最小值是( )
A. | B. | C. | D.5 |
已知 ,
,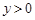 ,且
,且 ,则
,则 的最小值是 ( )
的最小值是 ( )
A.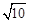 | B. | C. | D. |
若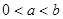 ,且
,且 ,则在下列四个选项中,最大的是( )
,则在下列四个选项中,最大的是( )
A. | B. | C. | D. |
 且满足
且满足 ,则
,则 的最小值为
的最小值为