题目内容
设函数y=f(x)满足对任意的x∈R,f(x)≥0且f2(x+1)+f2(x)=9.已知当x∈[0,1)时,有f(x)=2-|4x-2|,则f 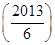 =________.
=________.
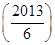 =________.
=________.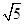
由题知f =2,因为f(x)≥0且f2(x+1)+f2(x)=9,故f
=2,因为f(x)≥0且f2(x+1)+f2(x)=9,故f =
=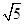 ,f
,f =2,f
=2,f =
=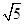 ,如此循环得f
,如此循环得f  =f
=f  =
=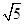 ,即f
,即f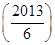 =
=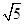
 =2,因为f(x)≥0且f2(x+1)+f2(x)=9,故f
=2,因为f(x)≥0且f2(x+1)+f2(x)=9,故f =
=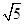 ,f
,f =2,f
=2,f =
=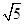 ,如此循环得f
,如此循环得f  =f
=f  =
=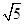 ,即f
,即f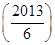 =
=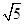

练习册系列答案
相关题目
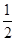 t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).
t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N). 上的零点个数为________.
上的零点个数为________.
 若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.
若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用. x2+10x(万元).当年产量不小于80千件时,C(x)=51x+
x2+10x(万元).当年产量不小于80千件时,C(x)=51x+ -1450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
-1450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完. ,则
,则 ( )
( )