题目内容
已知函数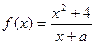 是奇函数。
是奇函数。
(1):求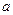 的值;
的值;
(2):当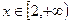 时,求
时,求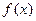 的反函数
的反函数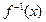 。
。
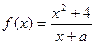 是奇函数。
是奇函数。(1):求
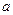 的值;
的值;(2):当
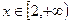 时,求
时,求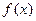 的反函数
的反函数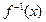 。
。 (1)0(2)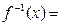
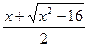
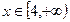
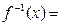
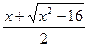
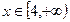
(1):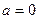
(2):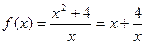 ,当
,当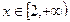 时,
时,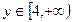
且反解得到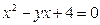 ,
,
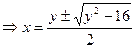 ,结合
,结合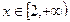
得到: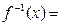
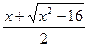
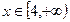
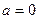
(2):
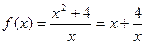 ,当
,当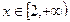 时,
时,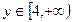
且反解得到
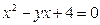 ,
,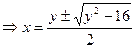 ,结合
,结合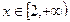
得到:
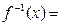
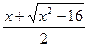
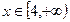

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
题目内容
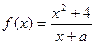 是奇函数。
是奇函数。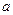 的值;
的值;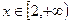 时,求
时,求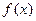 的反函数
的反函数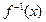 。
。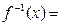
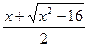
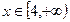
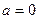
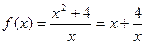 ,当
,当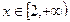 时,
时,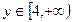
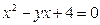 ,
,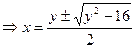 ,结合
,结合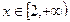
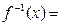
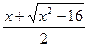
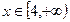

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案