题目内容
已知实系数一元二次方程 的两个实根为
的两个实根为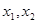 ,且
,且  ,则
,则 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
D
解析试题分析:由于实系数一元二次方程 的两个实根为
的两个实根为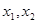 ,则判别式大于零,即
,则判别式大于零,即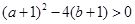
同时根据 ,则有
,则有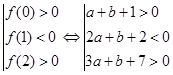 ,那么根据
,那么根据 的几何意义,表示的为区域内点(a,b)到原点(0,0)的斜率的范围,那么结合线性规划的知识可知,其结果为
的几何意义,表示的为区域内点(a,b)到原点(0,0)的斜率的范围,那么结合线性规划的知识可知,其结果为
故选D.
考点:本试题主要是考查了二次方程根的分布问题的运用。
点评:解决该试题的关键是利用二次函数的图像,同时结合开口和对称轴,以及端点值的函数值的符号,进而结合线性规划的知识确定出参数的范围,属于中档题。

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
幂函数 ,其中
,其中 ,且在(0,+∞)上是减函数,又
,且在(0,+∞)上是减函数,又 ,则
,则 =( )
=( )
| A.0 | B.1 | C.2 | D.3 |
已知幂函数 的图像经过
的图像经过 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
已知函数 为偶函数(0<θ<π), 其图象与直线y=2的交点的横坐标为
为偶函数(0<θ<π), 其图象与直线y=2的交点的横坐标为 的最小值为π,则( )
的最小值为π,则( )
A.ω=2,θ= | B.ω=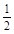 ,θ= ,θ= |
C.ω=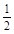 ,θ= ,θ= | D.ω=2,θ= |
幂函数 的图象经过点
的图象经过点 ( )
( )
A. | B. | C. | D. |
如果函数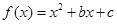 对任意实数均有
对任意实数均有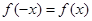 ,那么( )
,那么( )
A.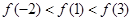 | B.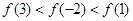 |
C.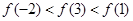 | D.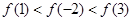 |
已知函数 ,则函数y=f(x)-log3x在(-1,3]上的零点的个数为
,则函数y=f(x)-log3x在(-1,3]上的零点的个数为
| A.4 | B.3 | C.2 | D.1 |
方程x3-6x2+9x-10=0的实根个数是( )
| A.3 | B.2 | C.1 | D.0 |
若 (其中
(其中 ),则函数
),则函数 的图象( )
的图象( )
| A.关于y轴对称 | B.关于X轴对称 |
| C.关于直线y=x轴称 | D.关于原点对称 |