题目内容
幂函数 ,其中
,其中 ,且在(0,+∞)上是减函数,又
,且在(0,+∞)上是减函数,又 ,则
,则 =( )
=( )
| A.0 | B.1 | C.2 | D.3 |
B
解析试题分析:根据题意,由于幂函数 ,其中
,其中 ,且在(0,+∞)上是减函数,又
,且在(0,+∞)上是减函数,又 ,因此是偶函数,那么对于选项A,不能符合题意,选项B,满足题意。选项C,由于是奇函数,不成立,选项D,由于m=3,函数y=x,是递增的,故选B.
,因此是偶函数,那么对于选项A,不能符合题意,选项B,满足题意。选项C,由于是奇函数,不成立,选项D,由于m=3,函数y=x,是递增的,故选B.
考点:幂函数的性质
点评:解决的关键是对于幂函数在第一象限内递减,说明幂指数小于零,同时是偶函数得到参数m的值,属于基础题。

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
对一元二次方程 的两个根的情况,判断正确的是
的两个根的情况,判断正确的是
| A.一根小于1,另一根大于3 | B.一根小于-2,另一根大于2 |
| C.两根都小于0 | D.两根都大于2 |
某人从2009年起,每年1月1日到银行新存入 元(一年定期),若年利率为
元(一年定期),若年利率为 保持不变,且每年到期存款和利息自动转为新的一年定期,到2012年底将所有存款及利息全部取回,则可取回的钱数(元)为
保持不变,且每年到期存款和利息自动转为新的一年定期,到2012年底将所有存款及利息全部取回,则可取回的钱数(元)为
A. | B. | C. | D. |
已知 函数
函数 的零点,若
的零点,若 ,则
,则 的值为( )
的值为( )
| A.恒为负值 | B.等于 | C.恒为正值 | D.不大于 |
若 ,且
,且 ,则
,则 的最大值是( )
的最大值是( )
| A.0 | B.1 | C.2 | D.4 |
下列式子正确的是 ( )
A. | B. |
C. | D. |
已知实系数一元二次方程 的两个实根为
的两个实根为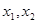 ,且
,且  ,则
,则 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
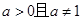 时,函数
时,函数 的图象只可能( )
的图象只可能( )
 )x的图象只可能是( )
)x的图象只可能是( )