题目内容
方程x3-6x2+9x-10=0的实根个数是( )
| A.3 | B.2 | C.1 | D.0 |
C
解析试题分析:由x3-6x2+9x-10=0得,x3=6x2-9x+10,画出y=x3,y=6x2-9x+10的图象,可知由图得一个交点.
故选C。.
考点:本题主要考查函数零点与方程的根个数的判断。
点评:数形结合是解决零点问题的有力工具,要善于将原问题转化成两个函数图象的交点问题是解决此问题的关键.数形结合是数学解题中常用的思想方法,能够变抽象思维为形象思维,有助于把握数学问题的本质.

练习册系列答案
相关题目
下列式子正确的是 ( )
A. | B. |
C. | D. |
已知实系数一元二次方程 的两个实根为
的两个实根为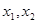 ,且
,且  ,则
,则 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
如图给出了函数 ,
, 的图象,则与函数
的图象,则与函数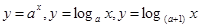 ,
, 依次对应的图象是( )
依次对应的图象是( )
| A.①②③④ | B.①③②④ |
| C.②③①④ | D.①④③② |
若 ,则
,则 属于区间( )
属于区间( )
A.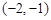 | B. | C. | D. |
下列各式中成立的一项( )
A. | B. |
C. | D. |
函数 满足
满足 ,且
,且 ,
, ,则下列等式不成立的是( )
,则下列等式不成立的是( )
A. | B. |
C. | D. |
函数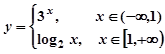 的值域为 ( )
的值域为 ( )
| A.(0,3) | B.[0,3] | C.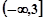 | D.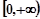 |
 的图象大致是( )
的图象大致是( )


