题目内容
过抛物线y2=4x的焦点作倾斜角为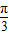
的直线与抛物线交于点A、B，则|AB|= ．
【答案】分析：求出抛物线的焦点坐标F（1，0），用点斜式设出直线方程：y=
，与抛物线方程联解得一个关于x的一元二次方程，利用根与系数的关系结合曲线的弦长的公式，可以求出线段AB的长度．
解答：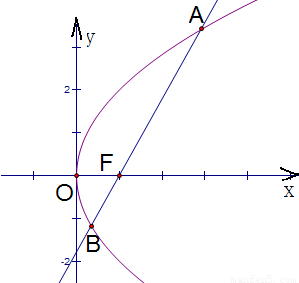
解：根据抛物线y2=4x方程得：焦点坐标F（1，0），
直线AB的斜率为k=tan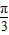
=
由直线方程的点斜式方程，设AB：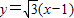
将直线方程代入到抛物线方程当中，得：3（x-1）2=4x
整理得：3x2-10x+3=0
设A（x1，y1），B（x2，y2）
由一元二次方程根与系数的关系得：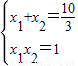
所以弦长|AB|=
=
故答案为
点评：本题以抛物线为载体，考查了圆锥曲线的弦长问题，属于难题．本题运用了直线方程与抛物线方程联解的方法，对运算的要求较高．利用一元二次方程根与系数的关系和弦长公式是解决本题的关键．
，与抛物线方程联解得一个关于x的一元二次方程，利用根与系数的关系结合曲线的弦长的公式，可以求出线段AB的长度．解答：
解：根据抛物线y2=4x方程得：焦点坐标F（1，0），直线AB的斜率为k=tan
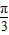=由直线方程的点斜式方程，设AB：
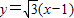
将直线方程代入到抛物线方程当中，得：3（x-1）2=4x
整理得：3x2-10x+3=0
设A（x1，y1），B（x2，y2）
由一元二次方程根与系数的关系得：
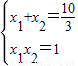
所以弦长|AB|=
=故答案为
点评：本题以抛物线为载体，考查了圆锥曲线的弦长问题，属于难题．本题运用了直线方程与抛物线方程联解的方法，对运算的要求较高．利用一元二次方程根与系数的关系和弦长公式是解决本题的关键．
练习册系列答案
活力课时同步练习册系列答案
学业测评一课一测系列答案
相关题目
倾斜角为
的直线过抛物线y2=4x的焦点且与抛物线交于A，B两点，则|AB|=（ ）
| π |
| 4 |
A、
| ||
B、8
| ||
| C、16 | ||
| D、8 |
过抛物线y2=4x的焦点F的直线交抛物线于A、B两点，点O是坐标原点，若|AF|=5，则△AOB的面积为（ ）
| A、5 | ||
B、
| ||
C、
| ||
D、
|