题目内容
已知函数f(x)=Acos(ωx+φ)+b(A>0,ω>0,|φ|<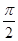 )在同一个周期内的图象上有一个最大值点A
)在同一个周期内的图象上有一个最大值点A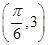 和一个最小值点B
和一个最小值点B .
.
(1)求f(x)的解析式;
(2)经过怎样的平移和伸缩变换可以将f(x)的图象变换为g(x)=cosx的图象.
【答案】
(1)f(x)=4cos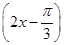 -1.(2)(一)将f(x)图象上各点向上平移1个单位;(二)将所得图象上各点横坐标伸长到原来的2倍,纵坐标缩短到原来的
-1.(2)(一)将f(x)图象上各点向上平移1个单位;(二)将所得图象上各点横坐标伸长到原来的2倍,纵坐标缩短到原来的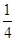 ;(三)将所得图象上各点左移
;(三)将所得图象上各点左移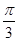 个单位,即可得到g(x)=cosx的图象.
个单位,即可得到g(x)=cosx的图象.
【解析】 (1)由f(x)的最大值点A与最小值点B可知,A=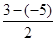 =4,b=
=4,b=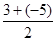 =-1,
=-1,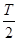 =
=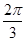 -
-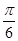 =
=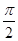 ,∴T=
,∴T=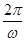 =π,∴ω=2.∴f(x)=4cos(2x+φ)-1.
=π,∴ω=2.∴f(x)=4cos(2x+φ)-1.
将点A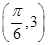 代入得:4cos
代入得:4cos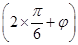 -1=3,
-1=3,
∴cos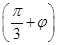 =1,
=1,
∴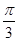 +φ=2kπ (k∈Z),∴φ=2kπ-
+φ=2kπ (k∈Z),∴φ=2kπ-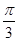 ,
,
∵|φ|<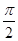 ,∴φ=-
,∴φ=-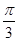 ,∴f(x)=4cos
,∴f(x)=4cos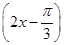 -1.
-1.
(2)依次按下列步骤变换:(一)将f(x)图象上各点向上平移1个单位;(二)将所得图象上各点横坐标伸长到原来的2倍,纵坐标缩短到原来的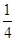 ;(三)将所得图象上各点左移
;(三)将所得图象上各点左移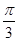 个单位,即可得到g(x)=cosx的图象.
个单位,即可得到g(x)=cosx的图象.

练习册系列答案
相关题目
 (a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4. .
. (a,b为常数,且a≠0),满足f(2)=1,方程f(x)=x有唯一实数解,求函数f(x)的解析式和f[f(-4)]的值.
(a,b为常数,且a≠0),满足f(2)=1,方程f(x)=x有唯一实数解,求函数f(x)的解析式和f[f(-4)]的值. )
)