题目内容
(本小题满分14分)
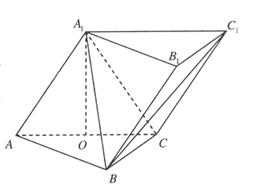
如图,在三棱柱![]() 中,侧面
中,侧面![]() 底面ABC,
底面ABC,![]() ,
,![]() ,且
,且![]() 为AC中点。
为AC中点。
证明:![]() 平面ABC;
平面ABC;
求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
在![]() 上是否存在一点E,使得
上是否存在一点E,使得![]() 平面
平面![]() ,若不存在,说明理由;若存在,确定点E的位置。
,若不存在,说明理由;若存在,确定点E的位置。
(Ⅰ)见解析(Ⅱ)![]() ,(Ⅲ)E为
,(Ⅲ)E为![]() 的中点
的中点
解析:
(Ⅰ)证明:因为![]() ,且O为AC的中点,
,且O为AC的中点,
所以![]() . ………………1分
. ………………1分
又由题意可知,平面![]() 平面
平面![]() ,交线为
,交线为![]() ,且
,且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() . ………………4分
. ………………4分
(Ⅱ)如图,以O为原点,![]() 所在直线分别为x,y,z轴建立空间直角坐标系.
所在直线分别为x,y,z轴建立空间直角坐标系.
由题意![]() 可知,
可知,![]() 又
又![]()
![]()
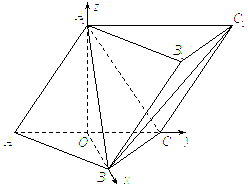 所以得:
所以得:![]()
则有:![]() ………………6分
………………6分
设平面![]() 的一个法向量为
的一个法向量为![]() ,则有
,则有
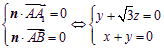 ,令
,令![]() ,得
,得![]()
所以![]() . ………………7分
. ………………7分
![]() . ………………9分
. ………………9分
因为直线![]() 与平面
与平面![]() 所成角
所成角![]() 和向量
和向量![]() 与
与![]() 所成锐角互余,所以
所成锐角互余,所以![]() . ………………10分
. ………………10分
(Ⅲ)设![]() ………………11分
………………11分
即![]() ,得
,得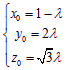
所以![]() 得
得![]() ………………12分
………………12分
令![]() 平面
平面![]() ,得
,得![]() , ………………13分
, ………………13分
即![]() 得
得![]()
即存在这样的点E,E为![]() 的中点. ………………14分
的中点. ………………14分

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)