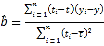题目内容
【题目】某市为调研学校师生的环境保护意识,决定在本市所有学校中随机抽取60所进行环境综合考评成绩达到80分以上(含80分)为达标.60所学校的考评结果频率分布直方图如图所示(其分组区间为[50,60),[60,70),[70,80),[80,90),[90,100]).

(Ⅰ)试根据样本估汁全市学校环境综合考评的达标率;
(Ⅱ)若考评成绩在[90.100]内为优秀.且甲乙两所学校考评结果均为优秀从考评结果为优秀的学校中随机地抽取两所学校作经验交流报告,求甲乙两所学校至少有一所被选中的概率.
【答案】(Ⅰ)0.35,(Ⅱ)甲乙两所学校至少有所被选中的概率P=![]() .
.
【解析】
试题(Ⅰ)根据频率分布直方图,计算即可.
(Ⅱ)先求出参加考评结果均为优秀的学校有0.10×60=6所,求概率,要一一列举出所有满足条件的基本事件根据古典概型的问题求其答案.
解:(Ⅰ)由频率分步直方图得,考评分不低于80的频率为:
1﹣0.05﹣0.2﹣0.4=0.35,
(Ⅱ)考评分在{90,100]的频率为0.1
所以参加考评结果均为优秀的学校有0.10×60=6所,
又已知甲乙两所学校考评结果均为优秀,
这6所学校分别记为:甲,乙,丙,丁,戊,己,故从中抽取2所共(甲乙),(甲丙),(甲丁),(甲戊),(甲己),(乙丙),(乙丁),(乙戊),(乙己),
(丙丁),(丙戊),(丙己),(丁戊),(丁己),(戊己)15种基本事件,
甲乙两所学校至少有所被选中的有(甲乙),(甲丙),(甲丁),(甲戊),(甲己),(乙丙),(乙丁),(乙戊),(乙己)9种基本事件.
所以甲乙两所学校至少有所被选中的概率P=![]() .
.

【题目】某大学生参加社会实践活动,对某公司1月份至6月份销售某种配件的销售量及销售单价进行了调查,销售单价![]() 和销售量
和销售量![]() 之间的一组数据如下表所示:
之间的一组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
销售量 | 11 | 10 | 8 | 6 | 5 | 14.2 |
(1)根据1至5月份的数据,先求出![]() 关于
关于![]() 的回归直线方程;6月份的数据作为检验数据.若由回归直线方程得到的预测数据与检验数据的误差不超过
的回归直线方程;6月份的数据作为检验数据.若由回归直线方程得到的预测数据与检验数据的误差不超过![]() ,则认为所得到的回归直线方程是理想的.试问所求得的回归直线方程是否理想?
,则认为所得到的回归直线方程是理想的.试问所求得的回归直线方程是否理想?
(2)预计在今后的销售中,销售量与销售单价仍然服从(1)中的回归关系,如果该种机器配件的成本是![]() 元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
参考数据:![]() ,
,![]() .
.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: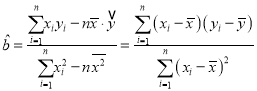 ,
,![]() .
.