题目内容
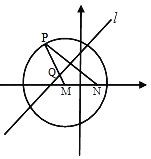
【题目】过直线2x+y+4=0和圆x2+y2+2x﹣4y+1=0的交点,且面积最小的圆方程为( )
A.(x+![]() )2+(y+
)2+(y+![]() )2=
)2=![]() B.(x﹣
B.(x﹣![]() )2+(y﹣
)2+(y﹣![]() )2=
)2=![]()
C.(x﹣![]() )2+(y+
)2+(y+![]() )2=
)2=![]() D.(x+
D.(x+![]() )2+(y﹣
)2+(y﹣![]() )2=
)2=![]()
【答案】D
【解析】
过直线与圆两交点面积最小的圆是以相交弦为直径的圆,由垂径定理求出相交弦长,以及相交弦的中点坐标,即可求解.
圆x2+y2+2x﹣4y+1=0即 (x+1)2+(y﹣2)2=4,
表示以C(﹣1,2)为圆心,半径等于2的圆.
圆心![]() 到直线2x+y+4=0的距离为d=
到直线2x+y+4=0的距离为d=![]() ,
,
故弦长为2![]() =2
=2![]() ,
,
故当面积最小的圆的半径为![]() .
.
过点C且与2x+y+4=0垂直的直线为![]() ,
,
由![]() 求得
求得 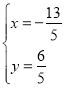 ,
,
即所求圆的圆心为(﹣![]() ,
,![]() ),
),
故所求的圆方程为:(x+![]() )2+(y﹣
)2+(y﹣![]() )2=
)2=![]() .
.
故选:D.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目