题目内容
如图,直角坐标平面内的正六边形ABCDEF,中心在原点,边长为a,AB平行于x轴,直线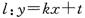 (k为常数)与正六边形交于M、N两点,记
(k为常数)与正六边形交于M、N两点,记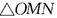 的面积为S,则关于函数
的面积为S,则关于函数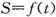 的奇偶性的判断正确的是 ( )
的奇偶性的判断正确的是 ( )
| A.一定是奇函数 |
| B.—定是偶函数 |
| C.既不是奇函数,也不是偶函数 |
| D.奇偶性与k有关 |
B
解析试题分析::∵当直线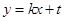 与
与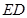 边重合时,
边重合时, ,当直线
,当直线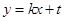 与
与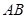 重合时,
重合时,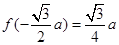 ,∴
,∴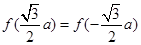 ,∵正六边形
,∵正六边形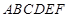 即是中心对称图形又是轴对称图形,
即是中心对称图形又是轴对称图形,
∴函数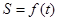 为偶函数.
为偶函数.
考点:1.函数的奇偶性;2.数形结合思想.

练习册系列答案
相关题目
设函数 ,其中
,其中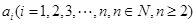 为已知实数,
为已知实数,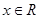 ,则下列各命题中错误的是( )
,则下列各命题中错误的是( )
A.若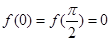 ,则 ,则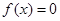 对任意实数恒成立; 对任意实数恒成立; |
B.若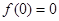 ,则函数 ,则函数 为奇函数; 为奇函数; |
C.若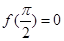 ,则函数 ,则函数 为偶函数; 为偶函数; |
D.当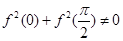 时,若 时,若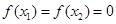 ,则 ,则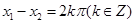 |
已知定义域为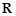 的函数
的函数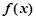 在区间
在区间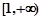 上单调递减,并且函数
上单调递减,并且函数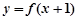 为偶函数,则下列不等式关系成立的是( )
为偶函数,则下列不等式关系成立的是( )
A.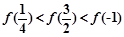 | B.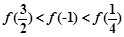 |
C.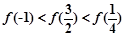 | D.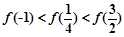 |
函数f(x)= +lg(-3x2+5x+2)的定义域是 ( )
+lg(-3x2+5x+2)的定义域是 ( )
A.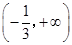 | B.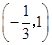 | C.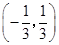 | D.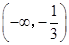 |
已知偶函数 在区间
在区间 单调增加,则满足
单调增加,则满足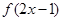 <
<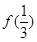 的
的 取值范围是( )
取值范围是( )
A.(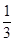 , ,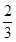 ) ) | B.[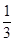 , ,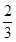 ) ) | C.(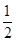 , ,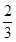 ) ) | D.[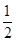 , ,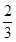 ) ) |
已知函数f(x)在R上为奇函数,对任意的 ,总有
,总有 且
且 ,则不等式
,则不等式 <0的解集为 ( )
<0的解集为 ( )
| A.(-1,0)∪(1,+∞) | B.(-∞,-1)∪(0,1) |
| C.(-∞,-1)∪(1,+∞) | D.(-1,0)∪(0,1) |
若函数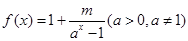 是奇函数,则
是奇函数,则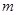 为
为
A.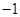 | B.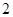 | C.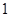 | D.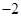 |
函数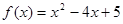 在区间
在区间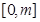 上的最大值为5,最小值为1,则实数m的取值范围是( )
上的最大值为5,最小值为1,则实数m的取值范围是( )
A.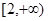 | B.[2,4] | C.[0,4] | D.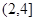 |
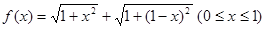 的性质,构造了如图所示的两个边长为
的性质,构造了如图所示的两个边长为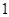 的正方形
的正方形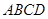 和
和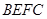 ,点
,点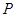 是边
是边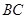 上的一个动点,设
上的一个动点,设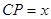 ,则
,则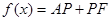 .那么可推知方程
.那么可推知方程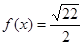 解的个数是( )
解的个数是( )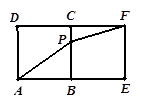
 .
. 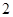 .
. 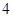 .
.