题目内容
2．
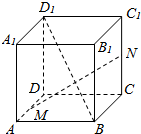如图所示，在正方体ABCD一A1B1C1D1中，取$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$作为基底．（1）求$\overrightarrow{B{D}_{1}}$；
（2）若有M，N分别为边AD，CC1的中点，求$\overrightarrow{MN}$．
分析 （1）根据向量加法的几何意义及相等向量和相反向量的概念便可得出$\overrightarrow{B{D}_{1}}=-\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$；
（2）根据向量加法的几何意义，以及向量数乘的几何意义便可用$\overrightarrow{a}，\overrightarrow{b}，\overrightarrow{c}$表示出$\overrightarrow{MN}$．
解答 解：（1）$\overrightarrow{B{D}_{1}}=\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{D{D}_{1}}$=$-\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$；
（2）$\overrightarrow{MN}=\overrightarrow{MD}+\overrightarrow{DC}+\overrightarrow{CN}$=$\frac{1}{2}\overrightarrow{b}+\overrightarrow{a}+\frac{1}{2}\overrightarrow{c}$．
点评 考查向量加法的几何意义，向量数乘的几何意义，以及相等向量和相反向量的概念．
练习册系列答案
相关题目
10．在△ABC中，内角A，B，C所对的边分别为a，b，c．已知cosB=-$\frac{1}{2}$．
（1）求sinAsinC的取值范围；
（2）若b=2$\sqrt{3}$，求△ABC面积的最大值．
（1）求sinAsinC的取值范围；
（2）若b=2$\sqrt{3}$，求△ABC面积的最大值．
17．设x是正数，则“a＞1”是“x+$\frac{a}{x}$＞1”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
17．已知直线l的参数方程为$\left\{\begin{array}{l}x=1+\frac{t}{2}\\ y=2+\frac{{\sqrt{3}}}{2}t\end{array}\right.$（t为参数），则其直角坐标方程为（ ）
| A． | $\sqrt{3}$x+y+2-$\sqrt{3}$=0 | B． | $\sqrt{3}$x-y+2-$\sqrt{3}$=0 | C． | x-$\sqrt{3}$y+2-$\sqrt{3}$=0 | D． | x+$\sqrt{3}$y+2-$\sqrt{3}$=0 |
18．如图所示描述错误的是（ ）
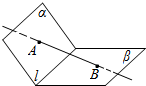
| A． | A∈α，B∈β | B． | α∩β=l | C． | AB∩α=A | D． | 直线AB与l相交 |