题目内容
【题目】已知{fn（x）}满足f1（x）= 
（x＞0），fn+1（x）=f1[fn（x）]，
（1）求f2（x），f3（x），并猜想fn（x）的表达式；
（2）用数学归纳法证明对fn（x）的猜想．
【答案】
（1）
解： 
猜想： 
，（n∈N*）
（2）
解：下面用数学归纳法证明 ，（n∈N*）
①当n=1时， 
，显然成立；②假设当n=k（k∈N*）时，猜想成立，即 
，
则当n=k+1时，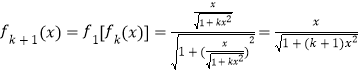 
即对n=k+1时，猜想也成立；
结合①②可知，猜想 对一切n∈N*都成立
【解析】（1）依题意，计算f2（x）=f1[f1（x）]可求得f2（x），同理可求f3（x）；（2）由（1）可猜想 ，然后用数学归纳法证明即可．
【考点精析】根据题目的已知条件，利用归纳推理和数学归纳法的定义的相关知识可以得到问题的答案，需要掌握根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理；数学归纳法是证明关于正整数n的命题的一种方法．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
