题目内容
在等比数列{an}中，a1＞1，公比q＞0，设bn=log2an，且b1+b3+b5=6，b1b3b5=0。
（1）求证：数列{bn}是等差数列；
（2）求数列{bn}的前n项和Sn及数列{an}的通项公式；
（3）试比较an与Sn的大小。
（1）求证：数列{bn}是等差数列；
（2）求数列{bn}的前n项和Sn及数列{an}的通项公式；
（3）试比较an与Sn的大小。
解：（1）由已知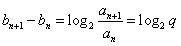
为常数，
故数列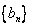
为等差数列，且公差为
（2）因
，
又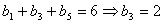
，
所以，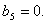
，
由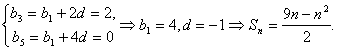
，
。
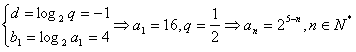（3）因为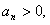
当n≥9时，
；
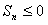所以，当n≥9时，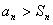
，
又可验证n=1，2时，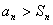
；n=3，4，5，6，7，8时，
。
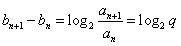为常数，故数列
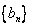为等差数列，且公差为 （2）因
，又
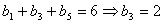，所以，
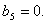，由
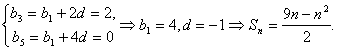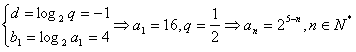，。（3）因为
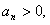当n≥9时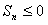，；所以，当n≥9时，
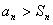，又可验证n=1，2时，
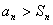；n=3，4，5，6，7，8时，。
练习册系列答案
相关题目
在等比数列{an}中，若a1=1，公比q=2，则a12+a22+…+an2=（ ）
| A、（2n-1）2 | ||
B、
| ||
| C、4n-1 | ||
D、
|