题目内容
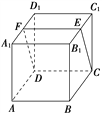
【题目】如图所示，在正方体ABCDA1B1C1D1中，E，F分别为B1C1，A1D1的中点．求证：平面ABB1A1与平面CDFE相交．
【答案】见解析
【解析】试题分析：由题意得EC与B1B不平行，则延长CE与BB1必须相交于一点，设为点H。然后证明点H为两平面的公共点，则由公理3可得平面ABB1A1与平面CDFE相交．
试题解析：
在正方体ABCDA1B1C1D1中，E为B1C1的中点，
所以EC与B1B不平行，
所以延长CE与BB1必须相交于一点，设为点H。
所以H∈EC，H∈B1B，
又B1B平面ABB1A1，CE平面CDFE，
所以H∈平面ABB1A1，H∈平面CDFE，
所以点H为平面ABB1A1与平面CDFE的公共点，
所以平面ABB1A1与平面CDFE相交．
练习册系列答案
相关题目
【题目】“菊花”型烟花是最壮观的烟花之一，制造时一般是期望在它达到最高点时爆裂．通过研究，发现该型烟花爆裂时距地面的高度
（单位：米）与时间
（单位：秒）存在函数关系，并得到相关数据如表：
时间 | 1 |
|
|
高度 |
|
|
|
（1）根据表中数据，从下列函数中选取一个函数描述该型烟花爆裂时距地面的高度
与时间
的变化关系： 
， 
， 
，确定此函数解析式并简单说明理由；
（2）利用你选取的函数，判断烟花爆裂的最佳时刻，并求此时烟花距地面的高度．
