题目内容
【题目】如图所示，ABCDA1B1C1D1是正方体，画出图中阴影部分的平面与平面ABCD的交线，并给出证明．
【答案】见解析
【解析】试题分析：过点E作EN⊥CD于点N，连接NB并延长，交EF的延长线于点M，连接AM，则直线AM为所求。证明时可证明点A，M同时在平面AEF和平面ABCD上即可。
试题解析：
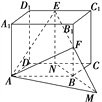
如图，过点E作EN⊥CD于点N，
连接NB并延长，交EF的延长线于点M，连接AM。
则直线AM即为图中阴影部分的平面与平面ABCD的交线。
证明如下：
因为直线EN∥BF，
所以B，N，E，F四点共面，
因此EF与BN相交，交点为M，
因为M∈EF，且M∈NB，
因为EF平面AEF，NB平面ABCD，
所以M是平面ABCD与平面AEF的公共点，
又因为点A是平面AEF和平面ABCD的公共点，
所以AM为这两平面的交线．
【题目】微信是现代生活进行信息交流的重要工具，若要调查某公司使用微信的员工经常使用微信与年龄的关系，并规定每天使用微信时间在一小时以上为经常使用微信。据统计，该公司200名员工中90%的人使用微信，其中不经常使用微信的有60人，其余经常使用微信。若将员工年龄分成青年（年龄小于40岁）和中年（年龄不小于40岁）两个阶段，使用微信的中75%是青年人.经常使用微信的员工中，有80人是青年人.
（1）请完成如下
联列表，
青年人 | 中年人 | 合计 | |
经常使用微信 | |||
不经常使用微信 | |||
合计 |
（2）由列联表中所得数据，是否有99.9%的把握认为“经常使用微信与年龄有关”？
（3）现采用分层抽样的方法从“经常使用微信的人”中抽取6人，从已抽取的这6人中任选2人，求“选出的2人均为青年人”的概率.
【题目】“菊花”型烟花是最壮观的烟花之一，制造时一般是期望在它达到最高点时爆裂．通过研究，发现该型烟花爆裂时距地面的高度
（单位：米）与时间
（单位：秒）存在函数关系，并得到相关数据如表：
时间 | 1 |
|
|
高度 |
|
|
|
（1）根据表中数据，从下列函数中选取一个函数描述该型烟花爆裂时距地面的高度
与时间
的变化关系： 
， 
， 
，确定此函数解析式并简单说明理由；
（2）利用你选取的函数，判断烟花爆裂的最佳时刻，并求此时烟花距地面的高度．
