题目内容
7．求下列函数的值域：y=$\frac{1-x}{2x+5}$，x∈[-3，-$\frac{5}{2}$）∪（一$\frac{5}{2}$，0]．
分析 把给出的函数解析式变形，然后利用函数图象的平移画出图形，数形结合求得函数的值域．
解答 解：由y=$\frac{1-x}{2x+5}$=$-\frac{x-1}{2x+5}$=$-\frac{\frac{1}{2}（2x+5）-\frac{7}{2}}{2x+5}$
=$\frac{7}{2（2x+5）}-\frac{1}{2}$=$\frac{7}{4（x+\frac{5}{2}）}-\frac{1}{2}$．
得其图象如图：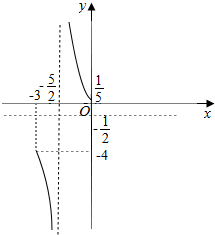
由图可知，函数y=$\frac{1-x}{2x+5}$，x∈[-3，-$\frac{5}{2}$）∪（一$\frac{5}{2}$，0]的值域为（-∞，-4]∪[$\frac{1}{5}，+∞$）．
点评 本题考查函数的值域，考查了数形结合的解题思想方法，属中档题．
练习册系列答案
小学课时特训系列答案
相关题目