题目内容
12.求证:函数f(x)=-x2+x在(-∞,$\frac{1}{2}$)上是单调递增函数.分析 定义法:任取x1<x2∈(-∞,$\frac{1}{2}$)且x1<x2,作差变形判断f(x1)-f(x2)<0可得结论.
解答 证明:任取x1<x2∈(-∞,$\frac{1}{2}$)且x1<x2,
作差可得f(x1)-f(x2)=(-x12+x1)-(-x22+x2)
=x22-x12+x1-x2=(x1-x2)(1-x1-x2),
∵x1<x2∈(-∞,$\frac{1}{2}$)且x1<x2,
∴x1-x2<0,1-x1-x2>0,
∴(x1-x2)(1-x1-x2)<0,
∴f(x1)<f(x2),
∴函数f(x)=-x2+x在(-∞,$\frac{1}{2}$)上是单调递增函数
点评 本题考查函数的单调性的判断和证明,涉及定义法证明函数的单调性,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知锐角△ABC中,A=2B,AC=2,则BC的范围为( )
| A. | (2$\sqrt{2}$,2$\sqrt{3}$) | B. | ($\sqrt{2}$,$\sqrt{3}$) | C. | ($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$) | D. | [2$\sqrt{2}$,2$\sqrt{3}$] |
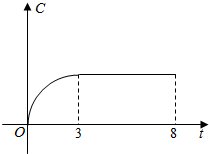 某工厂近8年来产品总量C与时间t(年)的关系如图所示,则下列说法中正确的序号是②③.
某工厂近8年来产品总量C与时间t(年)的关系如图所示,则下列说法中正确的序号是②③.