题目内容
【题目】在直三棱柱 ![]() 中,底面
中,底面 ![]() 是边长为2的正三角形,
是边长为2的正三角形, ![]() 是棱
是棱 ![]() 的中点,且
的中点,且 ![]() .
.
(1)试在棱 ![]() 上确定一点
上确定一点 ![]() ,使
,使 ![]() 平面
平面 ![]() ;
;
(2)当点 ![]() 在棱
在棱 ![]() 中点时,求直线
中点时,求直线 ![]() 与平面
与平面 ![]() 所成角的大小的正弦值。
所成角的大小的正弦值。
【答案】
(1)解:
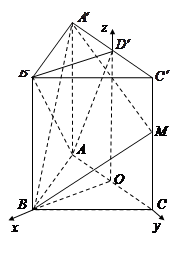
取AC边中点为O
∵底面ABC是边长为2的正三角形,∴ ![]()
连接 ![]() ,∵
,∵ ![]() 是边
是边 ![]() 的中点
的中点
∴ ![]() ,
, ![]()
所以可以建立以O为坐标原点,OB为x轴,OC为y轴,
![]() 为z轴如图所示的坐标系
为z轴如图所示的坐标系
则有 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]()
设 ![]() ,则
,则 ![]() ,
, ![]() ,
, ![]()
若 ![]() ,则有
,则有 ![]() ,
, ![]()
∴ 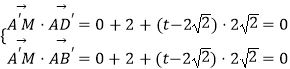 可得
可得 ![]()
即当 ![]() 时,
时, ![]()
(2)解:当点M棱 ![]() 中点时:
中点时: ![]()
∴ ![]() ,
, ![]() ,设平面
,设平面 ![]() 的一个法向量
的一个法向量 ![]()
∴ 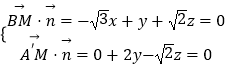 令
令 ![]() ,得
,得 ![]() ,
, ![]()
∴ ![]()
设直线 ![]() 与平面
与平面 ![]() 所成角为
所成角为 ![]() ,则
,则 ![]()
![]()
所以直线 ![]() 与平面
与平面 ![]() 所成角
所成角 ![]() 的正弦值为
的正弦值为 ![]()
【解析】(1)根据题意建立以O为坐标原点,OB为x轴,OC为y轴,![]() 为z轴如图所示的坐标系,求出各个点的坐标再设出点M的坐标利用向量的数量积等于零求出t的值,进而得出CM的值。(2)根据题意建立空间直角坐标系,求出各个点的坐标进而求出各个向量的坐标,设出平面A’BM的法向量,由向量垂直的坐标运算公式可求出法向量,再利用向量的数量积运算公式
为z轴如图所示的坐标系,求出各个点的坐标再设出点M的坐标利用向量的数量积等于零求出t的值,进而得出CM的值。(2)根据题意建立空间直角坐标系,求出各个点的坐标进而求出各个向量的坐标,设出平面A’BM的法向量,由向量垂直的坐标运算公式可求出法向量,再利用向量的数量积运算公式![]() 求出余弦值再利用同角三角函数的关系式求出正弦值。
求出余弦值再利用同角三角函数的关系式求出正弦值。

练习册系列答案
相关题目
【题目】某公司为了了解一年内的用水情况,抽取了10天的用水量如下表所示:
天数 | 1 | 1 | 1 | 2 | 2 | 1 | 2 |
用水量/吨 | 22 | 38 | 40 | 41 | 44 | 50 | 95 |
(Ⅰ)在这10天中,该公司用水量的平均数是多少?每天用水量的中位数是多少?
(Ⅱ)你认为应该用平均数和中位数中的哪一个数来描述该公司每天的用水量?