题目内容
4.已知椭圆C的中心为原点,焦点F1,F2在x轴上,焦距为6,过F1的直线l交椭圆C于A,B两点,且ABF2的周长为16,那么椭圆C的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{7}$=1.分析 由题意可得c=3,再由椭圆的定义与性质,求出a、b的值,即可写出椭圆的方程.
解答 解:设椭圆的长轴是2a,短轴是2b,焦距是2c,
由题意可得2c=6,解得c=3,
∴由椭圆的定义可得4a=|AF1|+|AF2|+|BF1|+|BF2|=16,
∴a=4,
∴b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{16-9}$=$\sqrt{7}$,
∴椭圆的方程是$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{7}$=1.
故答案为:$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{7}$=1.
点评 本题考查椭圆的定义和性质,注意运用椭圆的定义法是解题的关键,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.某射手平时射击成绩统计如表:
已知他射中7环及7环以下的概率为0.29.
(1)求a和b的值;
(2)求命中10环或9环的概率;
(3)求命中环数不足9环的概率.
| 环数 | 7环以下 | 7 | 8 | 9 | 10 |
| 概率 | 0.13 | a | b | 0.25 | 0.24 |
(1)求a和b的值;
(2)求命中10环或9环的概率;
(3)求命中环数不足9环的概率.
13.若a<b<0,则下列结论一定正确的是( )
| A. | $\frac{a+b}{2}$>$\sqrt{ab}$ | B. | $\frac{1}{|a|}$>$\frac{1}{|b|}$ | C. | ac2<bc2 | D. | (a+$\frac{1}{b}$)2>(b+$\frac{1}{a}$)2 |
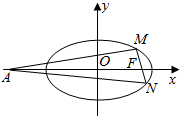 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,焦距为4,定点A(-4,0).
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,焦距为4,定点A(-4,0). 如图,O为坐标原点,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1F2,离心率为e1;双曲线C2:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为3F4,离心率为e2,已知e1e2=$\frac{\sqrt{3}}{2}$,且|F2F4|=$\sqrt{3}$-1.
如图,O为坐标原点,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1F2,离心率为e1;双曲线C2:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为3F4,离心率为e2,已知e1e2=$\frac{\sqrt{3}}{2}$,且|F2F4|=$\sqrt{3}$-1.