题目内容

【题目】如图，在四棱锥 中，平面PAD⊥ABCD，AB=AD，∠BAD=60°，E，F分别是AP，AD的中点.

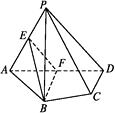
求证：
（1）直线EF∥平面PCD；
（2）平面BEF⊥平面PAD.

【答案】
（1）证明：在△PAD中，因为E，F分别为AP，AD的中点，所以EF∥PD.
又EF平面PCD，PD平面PCD，所以直线EF∥平面PCD
（2）证明：连接BD.因为AB=AD，∠BAD=60°，所以△ABD是正三角形.因为F是AD的中点，所以BF⊥AD.因为平面PAD⊥平面ABCD，BF平面ABCD，平面PAD∩平面ABCD=AD，所以BF⊥平面PAD.又因为BF平面BEF，所以平面BEF⊥平面PAD.

【解析】(1)要证明直线EF∥平面PCD,则要在平面PCD内找到直线PD与直线EF平行;
(2)要证明平面BEF⊥平面PAD,则要在其中一个平面BEF内找到直线BF与另一个平面PAD垂直.

练习册系列答案
相关题目

【题目】已知函数 ．（Ⅰ）求函数 的最小正周期及单调递增区间；（Ⅱ）将 的图像向右平移 个单位得到函数 的图像，若 ，求函数 的值域．

【题目】调查了某地若干户家庭的年收入x(单位：万元)和年饮食支出y(单位：万元)，调查显示年收入x与年饮食支出y具有线性相关关系，并由调查数据得到y对x的回归直线方程： ＝0. 254x＋0. 321. 由回归直线方程可知，家庭年收入每增加1万元，年饮食支出平均增加万元.

【题目】某单位最近组织了一次健身活动，活动分为登山组和游泳组，且每个职工至多参加其中一组．在参加活动的职工中，青年人占42. 5%，中年人占47. 5%，老年人占10%. 登山组的职工占参加活动总人数的 ，且该组中，青年人占50%，中年人占40%，老年人占10%. 为了了解各组不同年龄层次的职工对本次活动的满意程度，现用分层抽样方法从参加活动的全体职工中抽取一个容量为200的样本．试确定：
（1）游泳组中，青年人、中年人、老年人分别所占的比例；
（2）游泳组中，青年人、中年人、老年人分别应抽取的人数．

【题目】在平面直角坐标系xOy中，曲线C的参数方程为 （α为参数）．以坐标原点为极点，以x轴的正半轴为极轴，建立极坐标系，直线l的极坐标方程为 ． （Ⅰ）求直线l的直角坐标方程和曲线C的普通方程；
（Ⅱ）设点P为曲线C上任意一点，求点P到直线l的距离的最大值．

【题目】已知函数f（x）=2x3+3ax2+3bx+8在x=1及x=2处取得极值．
（1）求a、b的值；
（2）求f（x）的单调区间．

【题目】已知函数f（x）=lnx﹣ （m∈R）在区间[1，e]取得最小值4，则m= ．

【题目】设函数f（x）=x3﹣3ax+b．
（1）若曲线y=f（x）在点（2，f（x））处与直线y=8相切，求a，b的值．
（2）在（1）的条件下求函数f（x）的单调区间与极值点．

【题目】设函数 （ 且 ），当点 是函数 图象上的点时，点 是函数 图象上的点.
（1）写出函数 的解析式；
（2）把 的图象向左平移a个单位得到 的图象，函数 ，是否存在实数 ，使函数 的定义域为 ，值域为 .如果存在，求出 的值；如果不存在，说明理由；
（3）若当 时，恒有 ，试确定a的取值范围.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网