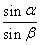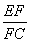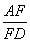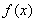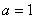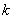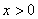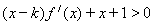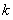题目内容
(拓展深化)如图①所示,△ABC内接于⊙O,AB=AC,D是BC边上的一点,E是直线AD和△ABC外接圆的交点.
(1)求证:AB2=AD·AE;
(2)如图②所示,当D为BC延长线上的一点时,第(1)题的结论成立吗?若成立,请证明;若不成立,请说明理由.
见解析
【解析】
证明 (1)如图③,连接BE.
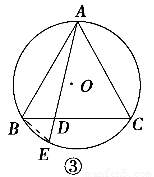
∵AB=AC,∴∠ABC=∠ACB.
∵∠ACB=∠AEB,
∴∠ABC=∠AEB.
∴△ABD∽△AEB.
∴AB∶AE=AD∶AB,
即AB2=AD·AE.
(2)如图④,连接BE、EC,
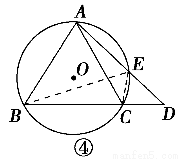
∵四边形ABCE内接于⊙O,
∴∠CED=∠ABC,
∵AB=AC,∴∠ABC=∠ACB,
∴∠CED=∠ACB,
∵∠AEC=180°-∠CED,
∠ACD=180°-∠ACB,
∴∠AEC=∠ACD,∴△ACE∽△ADC,
∴=,∴AB2=AD·AE.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目