题目内容
已知-1≤x≤2,求函数f(x)=3+2·3x+1-9x的值域.
函数f(x)的值域为[-24,12].
解析试题分析:利用换元法,转化为二次函数,利用配方法,根据函数的定义域,即可求得函数f(x)的值域.
解:f(x)=3+2·3x+1-9x=-(3x)2+6·3x+3.
令3x=t,
则y=-t2+6t+3=-(t-3)2+12.
∵-1≤x≤2,∴ ≤t≤9. ------------------------6分
≤t≤9. ------------------------6分
∴当t=3,即x=1时,y取得最大值12;
当t=9,即x=2时,y取得最小值-24,
即f(x)的最大值为12,最小值为-24.
∴函数f(x)的值域为[-24,12]. -----------------12分
考点:本题主要考查了二次函数的最值问题的研究。
点评:解决该试题的关键是函数值域的求解,考查换元法的运用,运用换元转化为二次函数求值域问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
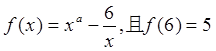
 的奇偶性;
的奇偶性;
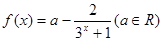 :
:  是
是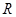 上的增函数;
上的增函数;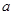 使函数
使函数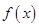 是偶函数,且
是偶函数,且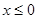 时,
时,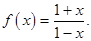 。
。 >0时
>0时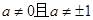 ,证明:
,证明:
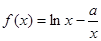 。
。 的单调区间;
的单调区间;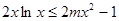 在
在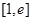 恒成立,求
恒成立,求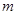 的取值范围。
的取值范围。
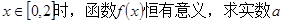 的取值范围;
的取值范围;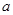 ,使得函数
,使得函数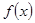 在区间
在区间 上为减函数,且最大值为1,若存在,求出
上为减函数,且最大值为1,若存在,求出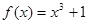 为R上的单调递增函数
为R上的单调递增函数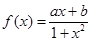 是定义在
是定义在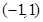 上的奇函数,且
上的奇函数,且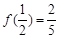 。
。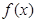 的解析式;
的解析式;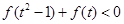 。
。 :
: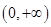 为单调递减函数;
为单调递减函数;  的奇偶性.
的奇偶性.