题目内容
(本小题满分14分)
已知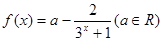 :
:
(1)用定义法证明函数 是
是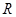 上的增函数;
上的增函数;
(2)是否存在实数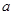 使函数
使函数 为奇函数?若存在,请求出
为奇函数?若存在,请求出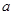 的值,若不存在,说明理由.
的值,若不存在,说明理由.
(1)见解析;(2)存在实数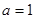 ,使函数
,使函数 为R上的奇函数。
为R上的奇函数。
解析试题分析:(1)设出变量,作差,变形,下结论,
(2)根据奇函数的性质,在x=0处 函数值为零,得到参数的值,进而加以证明。
(1)对任意 都有
都有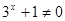 ,
,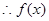 的定义域是R, -----------------2分
的定义域是R, -----------------2分
设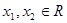 且
且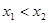 ,则
,则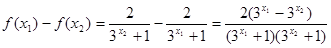 -----------------4分
-----------------4分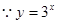 在R上是增函数,且
在R上是增函数,且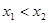

下面证明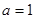 时
时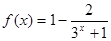 是奇函数
是奇函数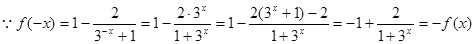
 为R上的奇函数
为R上的奇函数 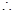 存在实数
存在实数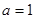 ,使函数
,使函数 为R上的奇函数。------14分
为R上的奇函数。------14分
考点:本题主要是考查函数单调性的证明,以及函数奇偶性的运用。
点评:解决该试题的关键是理解定义法证明函数单调性,现设出变量,和作差变形,然后利用奇函数的性质得到f(0)=0,得到a的值。

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
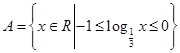 ,函数
,函数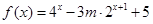 (其中
(其中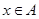 ,
, )
)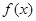 的定义域;
的定义域;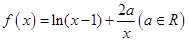 ,
,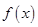 的图像在点
的图像在点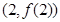 处的切线方程;
处的切线方程;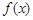 的单调区间;
的单调区间;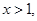 且
且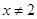 时,
时,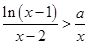 恒成立,求实数
恒成立,求实数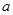 的取值范围。
的取值范围。 为定义在
为定义在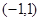 上的奇函数,当
上的奇函数,当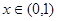 时,
时,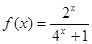 ;
;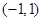 上的解析式;
上的解析式;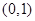 上的单调性,并给出证明.
上的单调性,并给出证明.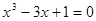 的根一个在
的根一个在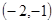 内,一个在
内,一个在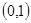 内,一个在
内,一个在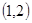 内.(12分)
内.(12分)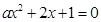 至少有一个负实根的充要条件。
至少有一个负实根的充要条件。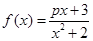 (其中
(其中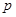 为常数,
为常数,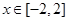 )为偶函数.
)为偶函数. 在
在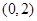 上是单调减函数;
上是单调减函数;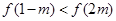 ,求实数
,求实数 的取值范围.
的取值范围.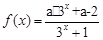 .
. 
 使函数f(x)为奇函数?证明你的结论;
使函数f(x)为奇函数?证明你的结论;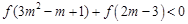 .
.