题目内容
(本题满分12分)已知函数
(1)当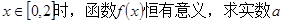 的取值范围;
的取值范围;
(2)是否存在这样的实数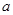 ,使得函数
,使得函数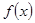 在区间
在区间 上为减函数,且最大值为1,若存在,求出
上为减函数,且最大值为1,若存在,求出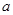 值;若不存在,说明理由。
值;若不存在,说明理由。
(1)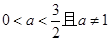 ;(2)这样的
;(2)这样的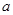 不存在。
不存在。
解析试题分析:(1)根据对数函数有意义可知,真数部分
 上恒成立,即
上恒成立,即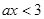 ,得到a的范围。
,得到a的范围。
(2)假设存在这样的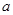
设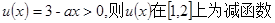 ,且有
,且有 ,可知外层为增函数,得到a的范围,进而求解最值。
,可知外层为增函数,得到a的范围,进而求解最值。
解:(1)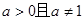 ,
, 
 上恒成立,即
上恒成立,即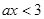
当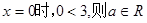
当
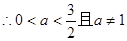 …………..4分
…………..4分
(2)假设存在这样的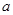
设 ,且有
,且有 ………..6分
………..6分
则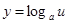 在区间内为增函数,
在区间内为增函数,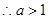 即
即 ………………8分
………………8分
而

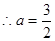 …………..10分
…………..10分 内,所以这样的
内,所以这样的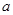 不存在……………12分
不存在……………12分
考点:本题主要考查对数函数的定义域和复合函数单调性的运用求解最值。
点评:解决该试题的关键是根据已知中恒有意义说明了最小值处 函数值大于零,同时根据存在a使得函数递减,则利用同增异减的思想得到a的取值情况。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
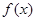 是定义在R上的奇函数,且
是定义在R上的奇函数,且 ,求:
,求: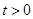 ,求函数
,求函数 上的最小值。
上的最小值。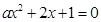 至少有一个负实根的充要条件。
至少有一个负实根的充要条件。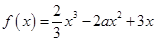 (
(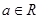 ).
).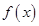 的单调区间;
的单调区间;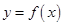 在
在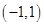 内有且只有一个极值点, 求a的取值范围.
内有且只有一个极值点, 求a的取值范围.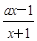 ,其中a∈R.
,其中a∈R.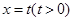 左侧的图形的面积为
左侧的图形的面积为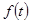 。试求函数
。试求函数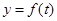 的图象.
的图象.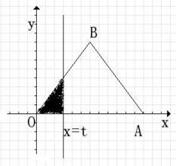
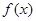 =
=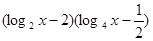 ,2≤
,2≤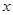 ≤4
≤4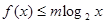 对于
对于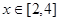 恒成立,求
恒成立,求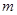 的取值范围.
的取值范围. 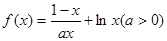
 在
在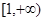 上为增函数,求实数
上为增函数,求实数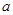 的取值范围
的取值范围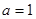 时,求
时,求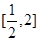 上的最大值和最小值
上的最大值和最小值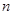 ,
,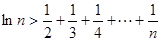 恒成立
恒成立