题目内容
(12分)已知函数 :
:
(1)写出此函数的定义域和值域;
(2)证明函数在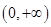 为单调递减函数;
为单调递减函数;
(3)试判断并证明函数 的奇偶性.
的奇偶性.
(1)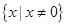 (2)见解析(3)奇函数
(2)见解析(3)奇函数
解析试题分析:(1)显然定义域为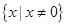 . ……3分
. ……3分
因为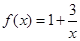 ∴值域为
∴值域为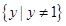 ……6分
……6分
(2)设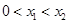 ,
,
则: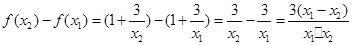 ,
,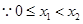 ∴
∴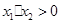 ,
, ,
,
∴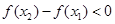 ,
,
∴函数在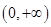 为单调递减函数. ……9分
为单调递减函数. ……9分
(3)显然函数定义域关于原点对称,
设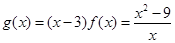 ,
, ,
,
∴此函数为奇函数. ……12分
考点:本小题主要考查函数定义域、值域的求法,用定义证明单调性以及函数奇偶性的判断.
点评:用定义证明单调性时一定要把结果化到最简,判断函数奇偶性时,要先看函数的定义域是否关于原点对称.

练习册系列答案
相关题目
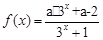 .
. 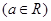
 使函数f(x)为奇函数?证明你的结论;
使函数f(x)为奇函数?证明你的结论;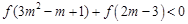 .
. 是定义在
是定义在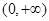 上的增函数,且对一切
上的增函数,且对一切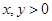 ,满足
,满足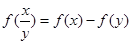 .
.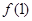 的值;
的值; ,解不等式
,解不等式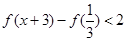
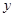 (毫克)与时间
(毫克)与时间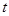 (小时)成正比.药物释放完毕后,
(小时)成正比.药物释放完毕后,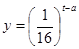 (
( 为常数),如图所示,根据图中提供的信息,回答下列问题:
为常数),如图所示,根据图中提供的信息,回答下列问题: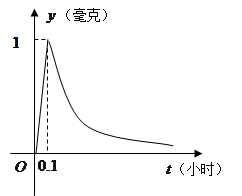
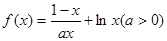
 在
在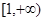 上为增函数,求实数
上为增函数,求实数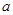 的取值范围
的取值范围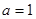 时,求
时,求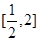 上的最大值和最小值
上的最大值和最小值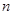 ,
,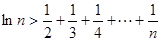 恒成立
恒成立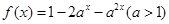
 的值域;
的值域;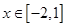 时,函数
时,函数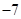 ,求
,求 的值和函数
的值和函数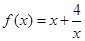
 在
在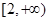 上为增函数;
上为增函数;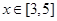 时,求函数
时,求函数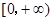 是定义在上的减函数,且
是定义在上的减函数,且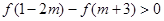 ,求实数
,求实数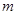 的取值范围。
的取值范围。