Question

【题目】已知递增数列{an}前n项和为Sn，且满足a1＝3，4Sn﹣4n+1＝an2，设bn（n∈N*)且数列{bn}的前n项和为Tn

（Ⅰ)求证：数列{an}为等差数列；

（Ⅱ)若对任意的n∈N*，不等式λTnn（﹣1)n+1恒成立，求实数λ的取值范围．

Answer 1

【答案】（Ⅰ)见解析（Ⅱ)（﹣∞，14)．

【解析】

（Ⅰ)当n≥2时，由4Sn﹣4n+1＝an2，类比可得4Sn﹣1﹣4（n﹣1)+1＝an﹣12，两式相减，再化简整理可得（an+an﹣1﹣2)（an﹣an﹣1﹣2)＝0，即an+an﹣1﹣2＝0，或an﹣an﹣1﹣2＝0，根据数列{an}是递增数列可排除不符合题意的一项，即可证明结论；

（Ⅱ)先根据第（Ⅰ)题的结果计算出数列{an}的通项公式，以及数列{bn}的通项公式，然后运用裂项相消法计算出Tn的表达式，将Tn的表达式代入不等式，分离参变量可得λ（2n+3)[3n+2(﹣1)n+1]，构造数列{cn}：令cn(2n+3)[3n+2(﹣1)n+1]，通过分别对数列{cn}的奇偶项的单调性进行分析可得数列{cn}的最小项的值，即可得到实数λ的取值范围．

（Ⅰ)证明：依题意，当n≥2时，由4Sn﹣4n+1＝an2，可得

4Sn﹣1﹣4(n﹣1)+1＝an﹣12，

两式相减，可得

4an﹣4＝an2﹣an﹣12，

化简整理，得

(an+an﹣1﹣2)(an﹣an﹣1﹣2)＝0，

∴an+an﹣1﹣2＝0，或an﹣an﹣1﹣2＝0，

∵数列{an}是递增数列，

∴an≥an﹣1，则an+an﹣1≥2an﹣1≥2a1＝2×3＝6，

∴an+an﹣1﹣2＝0不符合题意，

∴an﹣an﹣1﹣2＝0，即an﹣an﹣1＝2，

∴数列{an}是首项为3，公差为2的等差数列．

（Ⅱ)由（Ⅰ)知，an＝3+2(n﹣1)＝2n+1，n∈N*，

则bn()，

故Tn＝b1+b2+…+bn

()()()

()

()

，

将Tn代入不等式，可得λn（﹣1)n+1，

化简整理，得

λ(2n+3)[3n+2(﹣1)n+1]，

构造数列{cn}：令cn(2n+3)[3n+2(﹣1)n+1]，则

①当n为奇数时，n+2为奇数，

cn(2n+3)[3n+2(﹣1)n+1] (2n+3)(3n+2)，

cn+2[2(n+2)+3][3(n+2)+2(﹣1)n+3] (2n+7)（3n+8)，

cn+2﹣cn(2n+7)(3n+8)(2n+3)(3n+2)

，

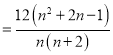∵n为奇数，∴n2+2n﹣10，

∴cn+2﹣cn0，即cn+2cn，

∴数列{cn}的奇数项为单调递增数列，即c1c3c5…

②当n为偶数时，n+2也为偶数，

cn(2n+3)[3n+2(﹣1)n+1]（2n+3)(3n﹣2)，

cn+2[2(n+2)+3][3(n+2)+2(﹣1)n+3] (2n+7)(3n+4)，

cn+2﹣cn(2n+7)(3n+4)(2n+3)(3n﹣2)

0，

故数列{cn}的偶数项为单调递增数列，即c2c4c6…

∵c1＝25，c2＝14，c3＝33，c4，

∴λ{cn}min＝c2＝14，

∴实数λ的取值范围为(﹣∞，14)．