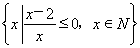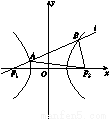题目内容
已知f(x)是定义域为R的奇函数,f(-4)=-1,f(x)的导函数f′(x)的图像如图X18-1所示.若两正数a,b满足f(a+2b)<1,则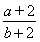 的取值范围是( )
的取值范围是( )

A. B.(-∞,-1) C.(-1,0) D.
B.(-∞,-1) C.(-1,0) D.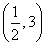
D
【解析】因为f(x)是定义域为R的奇函数,f(-4)=-1,所以f(4)=1.又因为f′(x)≥0恒成立,所以函数f(x)在R上单调递增.若两正数a,b满足f(a+2b)<1,则 把b看作横坐标,a看作纵坐标,则线性约束条件
把b看作横坐标,a看作纵坐标,则线性约束条件 的可行域是以点(0,0),(2,0),(0,4)为顶点的三角形.
的可行域是以点(0,0),(2,0),(0,4)为顶点的三角形. 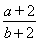 的几何意义为过点(-2,-2)和(b,a)的直线的斜率,由可行域知,当(b,a)为点(2,0)时,
的几何意义为过点(-2,-2)和(b,a)的直线的斜率,由可行域知,当(b,a)为点(2,0)时,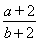 取最小值,其最小值为
取最小值,其最小值为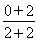 =
=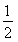 ;当(b,a)为点(0,4)时,
;当(b,a)为点(0,4)时,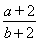 取最大值,其最大值为
取最大值,其最大值为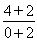 =3.故
=3.故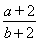 的取值范围是
的取值范围是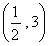 .
.

练习册系列答案
相关题目