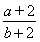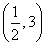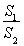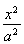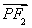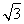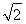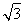Question

已知以点C为圆心的圆与x轴交于点O，A，与y轴交于点O，B，其中O为坐标原点．

(1)求证：△OAB的面积为定值；

(2)设直线y＝－2x＋4与圆C交于点M，N，若|OM|＝|ON|，求圆C的方程．

 

Answer 1

（1）见解析（2）(x－2)2＋(y－1)2＝5

【解析】(1)证明：因为圆与x轴交于点O，A，与y轴交于点O，B，所以△OAB是直角三角形．又圆心C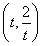，所以|OA|＝|2t|，|OB|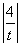＝，△OAB的面积为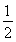|OA||OB|＝4，为定值．

(2)直线y＝－2x＋4与圆C交于点M，N，且|OM|＝|ON|，所以MN的中垂线是OC，OC的斜率为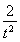，由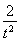×(－2)＝－1，得t＝2或t＝－2(舍)，则C(2，1)，OC即圆的半径，其长为.

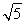故圆C的方程是(x－2)2＋(y－1)2＝5.