题目内容
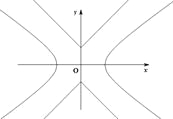
【题目】如图,已知曲线![]() ,曲线
,曲线![]() ,P是平面上一点,若存在过点P的直线与
,P是平面上一点,若存在过点P的直线与![]() 都有公共点,则称P为“C1—C2型点”.
都有公共点,则称P为“C1—C2型点”.
(1)在正确证明![]() 的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线![]() 与
与![]() 有公共点,求证
有公共点,求证![]() ,进而证明原点不是“C1—C2型点”;
,进而证明原点不是“C1—C2型点”;
(3)求证:圆![]() 内的点都不是“C1—C2型点”.
内的点都不是“C1—C2型点”.
【答案】见解析
【解析】
(1)C1的左焦点为![]() ,过F的直线
,过F的直线![]() 与C1交于
与C1交于![]() ,与C2交于
,与C2交于![]() ,故C1的左焦点为“C1-C2型点”,且直线可以为
,故C1的左焦点为“C1-C2型点”,且直线可以为![]() ;
;
(2)直线![]() 与C2有交点,则
与C2有交点,则
![]() ,若方程组有解,则必须
,若方程组有解,则必须![]() ;
;
直线![]() 与C2有交点,则
与C2有交点,则
![]() ,若方程组有解,则必须
,若方程组有解,则必须![]()
故直线![]() 至多与曲线C1和C2中的一条有交点,即原点不是“C1-C2型点”.
至多与曲线C1和C2中的一条有交点,即原点不是“C1-C2型点”.
(3)显然过圆![]() 内一点的直线
内一点的直线![]() 若与曲线C1有交点,则斜率必存在;
若与曲线C1有交点,则斜率必存在;
根据对称性,不妨设直线![]() 斜率存在且与曲线C2交于点
斜率存在且与曲线C2交于点![]() ,则
,则
![]()
直线![]() 与圆
与圆![]() 内部有交点,故
内部有交点,故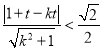
化简得,![]() ①
①
若直线![]() 与曲线C1有交点,则
与曲线C1有交点,则
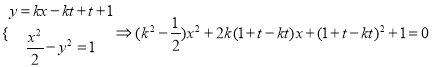
![]()
化简得,![]() ②
②
由①②得,![]()
但此时,因为![]() ,即①式不成立;
,即①式不成立;
当![]() 时,①式也不成立
时,①式也不成立
综上,直线![]() 若与圆
若与圆![]() 内有交点,则不可能同时与曲线C1和C2有交点,
内有交点,则不可能同时与曲线C1和C2有交点,
即圆![]() 内的点都不是“C1-C2型点” .
内的点都不是“C1-C2型点” .

练习册系列答案
相关题目
