题目内容
已知函数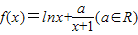 .
.(1)当
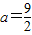 时,如果函数g(x)=f(x)-k仅有一个零点,求实数k的取值范围;
时,如果函数g(x)=f(x)-k仅有一个零点,求实数k的取值范围;(2)当a=2时,试比较f(x)与1的大小;
(3)求证:
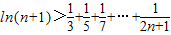 (n∈N*).
(n∈N*).
【答案】分析:(1)利用函数f(x)的导数求出它的单调区间和极值,由题意知 k大于f(x)的极大值,或 k小于f(x)的极小值.
(2)令h(x)=f(x)-1,由h′(x)>0得h(x)在(0,+∞)上是增函数,利用h(1)=0,分x>1、
0<x<1、当x=1三种情况进行讨论.
(3)根据(2)的结论,当x>1时,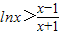 ,令
,令 ,有
,有 ,可得
,可得  ,由
,由 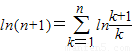 ,证得结论.
,证得结论.
解答:解:(1)当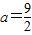 时,
时, ,定义域是(0,+∞),
,定义域是(0,+∞),
求得 ,令f'(x)=0,得
,令f'(x)=0,得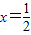 ,或x=2.
,或x=2.
∵当 或x>2时,f'(x)>0; 当
或x>2时,f'(x)>0; 当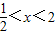 时,f'(x)<0,
时,f'(x)<0,
∴函数f(x)在(0, ]、(2,+∞)上单调递增,在
]、(2,+∞)上单调递增,在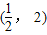 上单调递减.
上单调递减.
∴f(x)的极大值是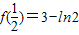 ,极小值是
,极小值是 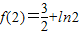 .
.
∵当x趋于 0时,f(x)趋于-∞;当x趋于+∞时,f(x)趋于+∞,
由于当g(x)仅有一个零点时,函数f(x)的图象和直线y=k仅有一个交点,
k的取值范围是{k|k>3-ln2,或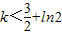 }.
}.
(2)当a=2时, ,定义域为(0,+∞).
,定义域为(0,+∞).
令 ,∵
,∵ ,
,
∴h(x)在(0,+∞)上是增函数. ①当x>1时,h(x)>h(1)=0,即f(x)>1;
②当0<x<1时,h(x)<h(1)=0,即f(x)<1; ③当x=1时,h(x)=h(1)=0,即f(x)=1.
(3)证明:根据(2)的结论,当x>1时, ,即
,即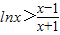 .
.
令 ,则有
,则有 ,∴
,∴ .
.
∵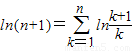 ,∴
,∴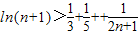 .
.
点评:本题主要考查函数导数运算法则、利用导数求函数的极值、证明不等式等基础知识,考查分类讨论思想和数形结合思想,考查考生的计算能力及分析问题、解决问题的能力和创新意识,属于中档题.
(2)令h(x)=f(x)-1,由h′(x)>0得h(x)在(0,+∞)上是增函数,利用h(1)=0,分x>1、
0<x<1、当x=1三种情况进行讨论.
(3)根据(2)的结论,当x>1时,
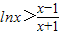 ,令
,令 ,有
,有 ,可得
,可得  ,由
,由 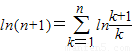 ,证得结论.
,证得结论.解答:解:(1)当
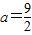 时,
时, ,定义域是(0,+∞),
,定义域是(0,+∞),求得
 ,令f'(x)=0,得
,令f'(x)=0,得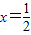 ,或x=2.
,或x=2.∵当
 或x>2时,f'(x)>0; 当
或x>2时,f'(x)>0; 当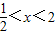 时,f'(x)<0,
时,f'(x)<0,∴函数f(x)在(0,
 ]、(2,+∞)上单调递增,在
]、(2,+∞)上单调递增,在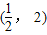 上单调递减.
上单调递减.∴f(x)的极大值是
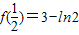 ,极小值是
,极小值是 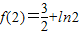 .
.∵当x趋于 0时,f(x)趋于-∞;当x趋于+∞时,f(x)趋于+∞,
由于当g(x)仅有一个零点时,函数f(x)的图象和直线y=k仅有一个交点,
k的取值范围是{k|k>3-ln2,或
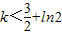 }.
}.(2)当a=2时,
 ,定义域为(0,+∞).
,定义域为(0,+∞).令
 ,∵
,∵ ,
,∴h(x)在(0,+∞)上是增函数. ①当x>1时,h(x)>h(1)=0,即f(x)>1;
②当0<x<1时,h(x)<h(1)=0,即f(x)<1; ③当x=1时,h(x)=h(1)=0,即f(x)=1.
(3)证明:根据(2)的结论,当x>1时,
 ,即
,即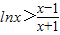 .
.令
 ,则有
,则有 ,∴
,∴ .
. ∵
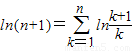 ,∴
,∴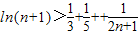 .
.点评:本题主要考查函数导数运算法则、利用导数求函数的极值、证明不等式等基础知识,考查分类讨论思想和数形结合思想,考查考生的计算能力及分析问题、解决问题的能力和创新意识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .
.  时,求函数
时,求函数 的定义域;
的定义域; 的不等式
的不等式 的解集是
的解集是 ,求
,求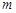 的取值范围.
的取值范围.
 。
。 时,判断
时,判断 的单调性;
的单调性; 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围;
的取值范围; .
. 时,求满足
时,求满足 的
的 的取值范围;
的取值范围; 的定义域为R,又是奇函数,求
的定义域为R,又是奇函数,求 .
. 时,如果函数
时,如果函数 仅有一个零点,求实数
仅有一个零点,求实数 的取值范围;
的取值范围; 时,试比较
时,试比较 与
与 的大小;
的大小; (
( ).
).