题目内容
（本小题12分）已知函数
。
（1）当
时，判断
的单调性；
（2）若
在其定义域内为增函数，求正实数
的取值范围；
【答案】
（1）
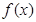在（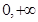
）上单调递增；（2）
.
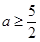【解析】第一问中利用由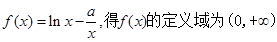
，
当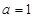 
时，
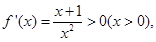
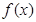在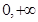（）上单调递增。
第二问由已知得，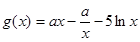
其定义域为（），
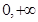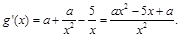
因为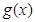
在其定义域内为增函数，所以
即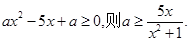
而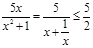
，当且仅当x=1时，等号成立，所以.
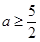解：由
，
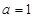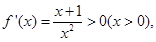
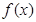当 时，在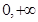（）上单调递增。
（2）由已知得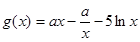，其定义域为（），
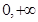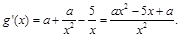
因为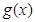在其定义域内为增函数，所以即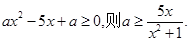
而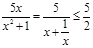，当且仅当x=1时，等号成立，所以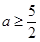
练习册系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
，
，直线
与函数
、
的k*s#5^u图象都相切，且与函数
.
的k*s#5^u值；
(其中
是
的k*s#5^u最大值；
时，求证：
.
中，
。
中，
，求数列
项和
.
轴上的抛物线与直线
交于P、Q两点，|PQ|=
，求抛物线的方程
；
过
且与圆C相切，求直线
，使直线
处的切线方程。