题目内容
【题目】已知曲线C的参数方程是 ![]() (α为参数),直线l的参数方程为
(α为参数),直线l的参数方程为  (t为参数),
(t为参数),
(1)求曲线C与直线l的普通方程;
(2)若直线l与曲线C相交于P,Q两点,且|PQ|= ![]() ,求实数m的值.
,求实数m的值.
【答案】
(1)解:∵曲线C的参数方程是 ![]() (α为参数),
(α为参数),
∴曲线C的普通方程:x2+(y﹣m)2=1,
∵直线l的参数方程为 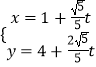 (t为参数),
(t为参数),
∴消去参数,得直线l的普通方程为:2x﹣y+2=0
(2)解:∵曲线C:x2+(y﹣m)2=1是以C(0,m)为圆心,以1为半径的圆,
圆心C(0,m)到直线l:2x﹣y+2=0的距离:d= ![]() =
= ![]() |m﹣2|,
|m﹣2|,
又直线l与曲线C相交于P,Q两点,且|PQ|= ![]() ,
,
∴2 ![]() =
= ![]()
解得m=1或m=3
【解析】(1)由sin2α+cos2α=1,能求出曲线C的普通方程,消去直线l中的参数,能求出直线l的普通方程.(2)求出圆心C(0,m)到直线l:2x﹣y+2=0的距离d,再由勾股定理结合弦长能求出m.

练习册系列答案
相关题目