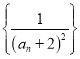题目内容
【题目】奇函数f(x)在R上存在导数![]() ,当x<0时,
,当x<0时,![]()
![]() f(x),则使得(x2﹣1)f(x)<0成立的x的取值范围为( )
f(x),则使得(x2﹣1)f(x)<0成立的x的取值范围为( )
A.(﹣1,0)∪(0,1)B.(﹣∞,﹣1)∪(0,1)
C.(﹣1,0)∪(1,+∞)D.(﹣∞,﹣1)∪(1,+∞)
【答案】C
【解析】
根据当x<0时,![]()
![]() f(x)的结构特征,构造函数
f(x)的结构特征,构造函数![]() ,求导得
,求导得![]() ,由当x<0时,
,由当x<0时,![]()
![]() f(x),得
f(x),得![]() 在
在![]() 上是减函数,再根据f(x)奇函数,则
上是减函数,再根据f(x)奇函数,则![]() 也是奇函数,
也是奇函数,![]() 在
在![]() 上也是减函数,又因为函数f(x)在R上存在导数
上也是减函数,又因为函数f(x)在R上存在导数![]() ,
,
所以函数f(x)是连续的,所以函数h(x)在R上是减函数,并且![]() 与
与![]() 同号,将(x2﹣1)f(x)<0转化为
同号,将(x2﹣1)f(x)<0转化为![]() 求解.
求解.
设![]() ,
,
所以![]() ,
,
因为当x<0时,![]()
![]() f(x),
f(x),
即![]() ,
,
所以![]() ,
,
所以![]() 在
在![]() 上是减函数.
上是减函数.
又因为f(x)奇函数,
所以![]() 也是奇函数,
也是奇函数,
所以![]() 在
在![]() 上也是减函数,
上也是减函数,
又因为函数f(x)在R上存在导数![]() ,
,
所以函数f(x)是连续的,
所以函数h(x)在R上是减函数,并且![]() 与
与![]() 同号,
同号,
所以(x2﹣1)f(x)<0![]()
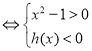 或
或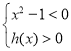
解得![]() 或
或![]()
故选:C

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目