题目内容
【题目】已知函数f(x)=(2log4x﹣2)(log4x﹣ ![]() ),
),
(1)当x∈[2,4]时,求该函数的值域;
(2)求f(x)在区间[2,t](t>2)上的最小值g(t).
【答案】
(1)解:令m=log4x,x∈[2,4]时,则m∈[ ![]() ,1],
,1],
则f(t)=(2m﹣2)(m﹣ ![]() )=2m2﹣3m+1=2(m﹣
)=2m2﹣3m+1=2(m﹣ ![]() )2﹣
)2﹣ ![]() ,
,
当m= ![]() 时,有最小值为﹣
时,有最小值为﹣ ![]() ,
,
当m= ![]() 或1时,有最大值为0,
或1时,有最大值为0,
∴该函数的值域为[﹣ ![]() ,0]
,0]
(2)解:由(1)可知f(m)=2m2﹣3m+1=2(m﹣ ![]() )2﹣
)2﹣ ![]() ,
,
∵x∈[2,t],
∴m∈[ ![]() ,log4t],
,log4t],
当 ![]() ≤m<
≤m< ![]() 时,即2≤t<2
时,即2≤t<2 ![]() 时,函数f(t)在[
时,函数f(t)在[ ![]() ,log4t],单调递减,
,log4t],单调递减,
g(t)=f(t)min=f(log4t)=2log42t﹣3log4t+1
当m≥ ![]() 时,即t≥2
时,即t≥2 ![]() 时,函数f(t)在[
时,函数f(t)在[ ![]() ,
, ![]() ]上单调递减,
]上单调递减,
在( ![]() ,log4t]单调递增,g(t)=f(t)min=f(
,log4t]单调递增,g(t)=f(t)min=f( ![]() )=﹣
)=﹣ ![]() ,
,
综上所述:g(t)= 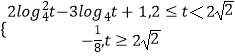
【解析】(1)令m=log4x,则可将函数在x∈[2,4]时的值域问题转化为二次函数在定区间上的值域问题;(2)根据二次函数的性质和对称轴,分类讨论即可求出最小值.
【考点精析】本题主要考查了函数的值域和函数的最值及其几何意义的相关知识点,需要掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的;利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值才能正确解答此题.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案【题目】共享单车是指企业在校园、地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务,是共享经济的一种新形态.一个共享单车企业在某个城市就“一天中一辆单车的平均成本(单位:元)与租用单车的数量(单位:千辆)之间的关系”进行调查研究,在调查过程中进行了统计,得出相关数据见下表:
租用单车数量 | 2 | 3 | 4 | 5 | 8 |
每天一辆车平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
根据以上数据,研究人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲: ![]() ,方程乙:
,方程乙: ![]() .
.
(1)为了评价两种模型的拟合效果,完成以下任务:
①完成下表(计算结果精确到0.1)(备注: ![]() ,
,![]() 称为相应于点
称为相应于点![]() 的残差(也叫随机误差));
的残差(也叫随机误差));
租用单车数量 | 2 | 3 | 4 | 5 | 8 | |
每天一辆车平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
模型甲 | 估计值 | 2.4 | 2.1 | 1.6 | ||
残差 | 0 | -0.1 | 0.1 | |||
模型乙 | 估计值 | 2.3 | 2 | 1.9 | ||
残差 | 0.1 | 0 | 0 | |||
②分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并通过比较
,并通过比较![]() 的大小,判断哪个模型拟合效果更好.
的大小,判断哪个模型拟合效果更好.
(2)这个公司在该城市投放共享单车后,受到广大市民的热烈欢迎,共享单车常常供不应求,于是该公司研究是否增加投放.根据市场调查,这个城市投放8千辆时,该公司平均一辆单车一天能收入10元,6元收入的概率分别为0.6,0.4;投放1万辆时,该公司平均一辆单车一天能收入10元,6元收入的概率分别为0.4,0.6.问该公司应该投放8千辆还是1万辆能获得更多利润?(按(1)中拟合效果较好的模型计算一天中一辆单车的平均成本,利润=收入-成本).