题目内容
13.若一元二次方程(m-1)x2+2(m+1)x-m=0有两个正根,求m的取值范围.分析 由条件利用二次函数的性质求得实数m取值的范围.
解答 解:关于x的一元二次方程(m一1)x2+2(m+1)x-m=0有两个正根,
∴$\left\{\begin{array}{l}{4(m+1)^{2}+4m(m-1)≥0}\\{-\frac{2(m+1)}{m-1}>0}\\{-\frac{m}{m-1}>0}\end{array}\right.$,求得0<m<1.
点评 本题主要考查一元二次方程根的分布与系数的关系,二次函数的性质,体现了转化的数学思想,属于基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
8.下列函数中,与函数y=-x的奇偶性,单调性都相同的是( )
| A. | y=$\frac{1}{x}$ | B. | y=-sinx | C. | y=-lnx | D. | y=lg($\sqrt{{x}^{2}+1}$-x) |
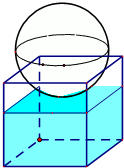 如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,求球的体积.
如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,求球的体积.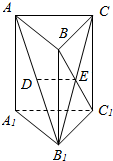 如图:在三棱柱ABC-A1B1C1中,已知AA1⊥底面ABC,AC⊥BC.四边形BB1C1C为正方形,设AB1的中点为D,B1C∩BC1=E.求证
如图:在三棱柱ABC-A1B1C1中,已知AA1⊥底面ABC,AC⊥BC.四边形BB1C1C为正方形,设AB1的中点为D,B1C∩BC1=E.求证