题目内容
已知函数y=f(x)在区间[a,b]上均有意义,且A、B是其图象上横坐标分别为a、b的两点.对应于区间[0,1]内的实数λ,取函数y=f(x)的图象上横坐标为x=λa+(1-λ)b的点M,和坐标平面上满足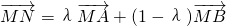 的点N,得
的点N,得 .对于实数k,如果不等式|MN|≤k对λ∈[0,1]恒成立,那么就称函数f(x)在[a,b]上“k阶线性近似”.若函数y=x2+x在[1,2]上“k阶线性近似”,则实数k的取值范围为
.对于实数k,如果不等式|MN|≤k对λ∈[0,1]恒成立,那么就称函数f(x)在[a,b]上“k阶线性近似”.若函数y=x2+x在[1,2]上“k阶线性近似”,则实数k的取值范围为
- A.
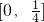
- B.[0,+∞)
- C.
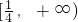
- D.
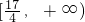
C
分析:先得出M、N横坐标相等,将恒成立问题转化为求函数的最值问题.
解答:由题意,M、N横坐标相等,不等式|MN|≤k对λ∈[0,1]恒成立,则k≥|MN|的最大值.
由A、B是其图象上横坐标分别为a、b的两点,则A(1,2),(2,6)
∴AB方程为y-6=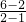 ×(x-2),即y=4x-2
×(x-2),即y=4x-2
由图象可知,|MN|=4x-2-(x2+x)=-(x- )2+
)2+ ≤
≤
∴k≥
故选C.
点评:本题考查新定义,解答的关键是将已知条件进行转化,同时应注意恒成立问题的处理策略.
分析:先得出M、N横坐标相等,将恒成立问题转化为求函数的最值问题.
解答:由题意,M、N横坐标相等,不等式|MN|≤k对λ∈[0,1]恒成立,则k≥|MN|的最大值.
由A、B是其图象上横坐标分别为a、b的两点,则A(1,2),(2,6)
∴AB方程为y-6=
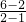 ×(x-2),即y=4x-2
×(x-2),即y=4x-2由图象可知,|MN|=4x-2-(x2+x)=-(x-
 )2+
)2+ ≤
≤
∴k≥

故选C.
点评:本题考查新定义,解答的关键是将已知条件进行转化,同时应注意恒成立问题的处理策略.

练习册系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足