题目内容
设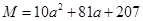 ,
,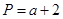 ,Q=
,Q= ;若将
;若将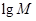 ,lgQ,lgP适当排序后可构成公差为1的等差数列
,lgQ,lgP适当排序后可构成公差为1的等差数列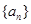 的前三项.
的前三项.
(1)试比较M、P、Q的大小;
(2)求 的值及
的值及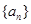 的通项;
的通项;
(3)记函数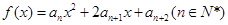 的图象在
的图象在 轴上截得的线段长为
轴上截得的线段长为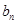 ,
,
设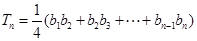
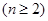 ,求
,求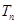 ,并证明
,并证明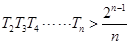 .
.
(1)当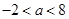 时:
时: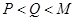 ;当
;当 时:
时: 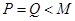 ;当
;当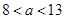 时:
时: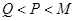 ;
;
(2)当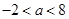 时:
时: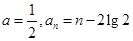 ;当
;当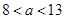 时:无解.
时:无解.
解析试题分析:(1)两两之间作差比较大小;(2)根据第(1)问的结果结合等差数列项的关系求解;(3)先求出线段长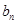 ,再表示出
,再表示出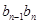 ,通过裂项相消化简求值
,通过裂项相消化简求值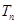 ,再结合放缩法求范围
,再结合放缩法求范围
试题解析:(1)由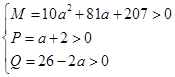 得
得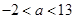 2分
2分 3分
3分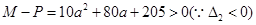 4分
4分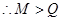 ,
,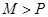
又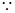 当
当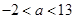 时,
时,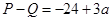 ,
,
当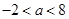 时,即
时,即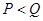 ,则
,则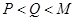 5分
5分
当 时,
时,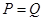 ,则
,则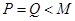
当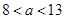 时,
时,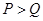 ,则
,则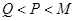
(2)当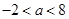 时,
时, 即
即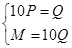

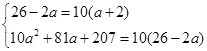
解得 ,从而
,从而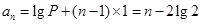 7分
7分
当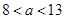 时,
时,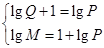 即
即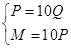

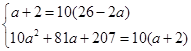 ,
,  无解. 8分
无解. 8分
(3)设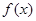 与
与 轴交点为
轴交点为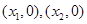
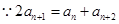 ,
, 当
当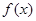 =0时有
=0时有
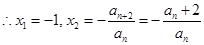 9分
9分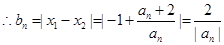
又 ,
,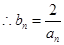
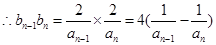
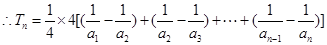
 11分
11分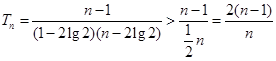
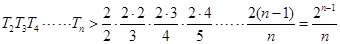 14分
14分
考点:1.作差比较大小;2.分类讨论思想;3.等差数列通项;4.裂项相消求和;5.放缩法应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
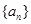 为等差数列,数列
为等差数列,数列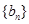 为等比数列且公比大于1,若
为等比数列且公比大于1,若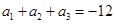 ,
,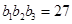 ,且
,且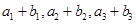 恰好是一各项均为正整数的等比数列的前三项.
恰好是一各项均为正整数的等比数列的前三项.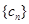 满足
满足
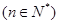 ,求
,求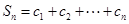 .
.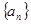 中,
中,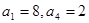 且满足
且满足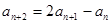 (
( 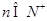 )
)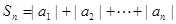 ,求
,求 ;
;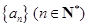 的前
的前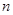 项和为
项和为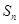 ,且
,且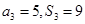 .
.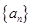 的通项公式;
的通项公式;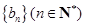 ,若
,若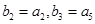 ,求数列
,求数列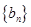 的前
的前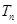 .
. (
(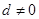 )的等差数列
)的等差数列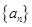 与公比为
与公比为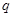 (
(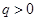 )的等比数列
)的等比数列 有如下关系:
有如下关系: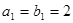 ,
,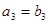 ,
,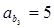 .
.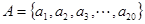 ,
,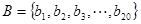 ,
,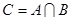 ,求集合
,求集合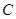 中的各元素之和。
中的各元素之和。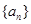 中,
中,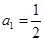 ,点
,点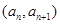 在直线
在直线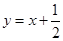 上.
上.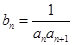 ,求数列
,求数列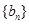 的前n项和
的前n项和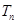 .
.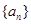 是公比大于
是公比大于 的等比数列,
的等比数列,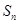 是
是 项和.若
项和.若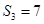 ,且
,且 ,
,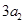 ,
, 构成等差数列.
构成等差数列.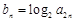 ,求数列
,求数列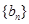 的前
的前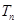 .
.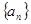 是一个等差 数列,且
是一个等差 数列,且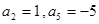 。
。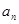 ; (2)求
; (2)求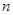 项和
项和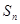 的最大值。
的最大值。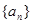 是等差数列,
是等差数列,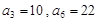 ,数列
,数列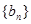 的前n项和是
的前n项和是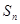 ,且
,且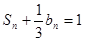 .
.