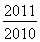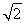题目内容
对于任意x∈[1,2]，都有(ax＋1)2≤4成立，则实数a的取值范围为________．
【解析】由不等式(ax＋1)2≤4在x∈[1,2]恒成立，得－2≤ax＋1≤2在x∈[1,2]恒成立，利用分类参数的方法得
利用反比例函数的单调性得－
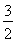≤a≤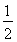
.
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
已知集合A、B，定义集合A与B的一种运算A⊕B，其结果如下表所示：
A | {1,2,3,4} | {－1,1} | {－4,8} | {－1,0,1} |
B | {2,3,6} | {－1,1} | {－4，－2,0,2} | {－2，－1,0,1} |
A⊕B | {1,4,6} | ∅ | {－2,0,2,8} | {－2} |
按照上述定义，若M＝{－2 011,0,2 012}，N＝{－2 012,0,2 013}，则M⊕N＝________.
