题目内容
2.如果实数x,y满足线性约束条件$\left\{{\begin{array}{l}{2x-y≤0}\\{x-3y+5≥0}\\{y≥1}\end{array}}\right.$,则z=x+y-2的最小值等于-3.分析 作出可行域,变形目标函数,平移直线y=-x可得当直线经过点A(-2,1)时,z取最小值,代值计算可得.
解答 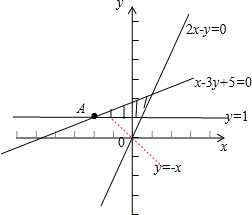 解:作出线性约束条件$\left\{{\begin{array}{l}{2x-y≤0}\\{x-3y+5≥0}\\{y≥1}\end{array}}\right.$所对应的可行域(如图),
解:作出线性约束条件$\left\{{\begin{array}{l}{2x-y≤0}\\{x-3y+5≥0}\\{y≥1}\end{array}}\right.$所对应的可行域(如图),
变形目标函数可得y=-x+2+z,平移直线y=-x可知,
当直线经过点A(-2,1)时,截距2+z取最小值,z取最小值,
代值计算可得z的最小值为z=-2+1-2=-3
故答案为:-3.
点评 本题考查简单线性规划,准确作图是解决问题的关键,属中档题.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
12. 如图,长方体ABCD-A′B′C′D′中,AB=BC=$\sqrt{2}$,AA$′=\sqrt{3}$,上底面A′B′C′D′的中心为O′,当点E在线段CC′上从C移动到C′时,点O′在平面BDE上的射影G的轨迹长度为( )
如图,长方体ABCD-A′B′C′D′中,AB=BC=$\sqrt{2}$,AA$′=\sqrt{3}$,上底面A′B′C′D′的中心为O′,当点E在线段CC′上从C移动到C′时,点O′在平面BDE上的射影G的轨迹长度为( )
 如图,长方体ABCD-A′B′C′D′中,AB=BC=$\sqrt{2}$,AA$′=\sqrt{3}$,上底面A′B′C′D′的中心为O′,当点E在线段CC′上从C移动到C′时,点O′在平面BDE上的射影G的轨迹长度为( )
如图,长方体ABCD-A′B′C′D′中,AB=BC=$\sqrt{2}$,AA$′=\sqrt{3}$,上底面A′B′C′D′的中心为O′,当点E在线段CC′上从C移动到C′时,点O′在平面BDE上的射影G的轨迹长度为( )| A. | $\frac{2π}{3}$ | B. | $\frac{\sqrt{3}}{3}π$ | C. | $\frac{π}{3}$ | D. | $\frac{\sqrt{3}π}{6}$ |
14. 已知某程序框图如图所示,那么执行该程序后输出的结果是( )
已知某程序框图如图所示,那么执行该程序后输出的结果是( )
 已知某程序框图如图所示,那么执行该程序后输出的结果是( )
已知某程序框图如图所示,那么执行该程序后输出的结果是( )| A. | $\frac{1}{2}$ | B. | 0 | C. | $-\frac{1}{2}$ | D. | -1 |